如图(1),凸四边形 ,如果点
,如果点 满足
满足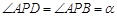 ,且
,且 ,则称点
,则称点 为四边形
为四边形 的一个半等角点.
的一个半等角点.在图(2)正方形
 内画一个半等角点
内画一个半等角点 ,且满足
,且满足 ;
;在图(3)四边形
 中画出一个半等角点
中画出一个半等角点 ,
,
保留画图痕迹(不需写出画法).

已知:如图,点 是以 为直径的 上异于 、 的任意一点.连接 并延长至 ,使 .连接 、 .过点 作 于 .
(1)求证: 是 的切线;
(2)求证: ;
(3)若 半径确定,当 的面积最大时,求 的值.

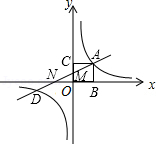
如图,正方形 的面积为4,反比例函数 的图象经过点 ,过点 的直线 与 的图象相交于第三象限的点 ,且点 到 轴的距离为4.
(1)求反比例函数 和一次函数 的解析式.
(2)当 时,观察函数 的图象,直接写出 的取值范围.
(3)直线 与坐标轴交于 、 两点,求 外接圆的面积.
为鼓励万众创新大众创业,市政府给予了招商引资企业的优惠政策,许多企业应运而生.招商局就今年一至五月招商情况绘制如下两幅不完全的统计图.

(1)该市今年一至五月招商引资企业一共有 家,请将条形统计图补充完整.
(2)从农业类和第三产业类企业中,任意抽取2家企业进行质量检测,请用列表或画树状图的方法,求抽中2家企业均为农业类的概率.
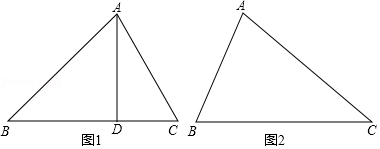
已知:如图1,在锐角 中, , , , 于 .
在 中, ,则 ;
在 中, ,则 ;
所以, ,即, ,
进一步即得正弦定理: (此定理适合任意锐角三角形).
参照利用正弦定理解答下题:
如图2,在 中, , , ,求 的长.
红旗连锁超市花2000购进一批糖果,按 的利润定价无人购买,决定降价出售,但仍无人购买.结果又一次降价后才售完,但仍盈利 ,两次降价的百分率相同,问每次降价的百分率是多少?