某商店销售洗衣粉,年销售总量为6000包,每包进价2.8元,销售价3.4元.全年分若干次进货,每次进货均为 包.已知每次进货运输劳务费为62.5元,全年保管费为1.5
包.已知每次进货运输劳务费为62.5元,全年保管费为1.5 元.
元.
(1)把该店经销洗衣粉一年的利润 (元)表示为每次进货量
(元)表示为每次进货量 (包)的函数,并指出函数的定义域;
(包)的函数,并指出函数的定义域;
(2)为了使利润最大化,问每次该进货多少包?
在 中,内角
中,内角 对边的边长分别是
对边的边长分别是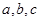 ,已知
,已知 ,
,
(1)若 的面积等于
的面积等于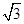 ,求
,求 ;
;
(2) ,求
,求 的面积。
的面积。
已知函数 ,(
,(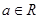 且
且 )。
)。
(1)设 ,令
,令 ,试判断函数
,试判断函数 在
在 上的单调性并证明你的结论;
上的单调性并证明你的结论;
(2)若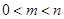 且
且
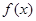 的定义域和值域都是
的定义域和值域都是 ,求
,求 的最大值;
的最大值;
(3)若不等式 对
对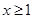 恒成立,求实数
恒成立,求实数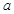 的取值范围;
的取值范围;
已知函数 ,
, 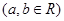
(1)当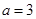 时, 若
时, 若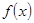 有
有 个零点, 求
个零点, 求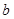 的取值范围;
的取值范围;
(2)对任意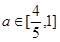 , 当
, 当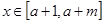 时恒有
时恒有 , 求
, 求 的最大值, 并求此时
的最大值, 并求此时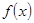 的最大值。
的最大值。
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量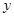 (升)关于行驶速度
(升)关于行驶速度 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: 已知甲、乙两地相距100千米。
已知甲、乙两地相距100千米。
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
设二次函数 ,方程
,方程 的两根
的两根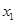 和
和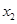 满足
满足 .
.
(1)求实数 的取值范围;
的取值范围;
(2)试比较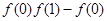 与
与 的大小.并说明理由.
的大小.并说明理由.