(本小题满分15分) 如图,设椭圆 的左、右焦点分别为
的左、右焦点分别为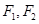 ,过
,过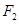
作直线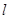 交椭圆与
交椭圆与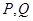 两点,若圆
两点,若圆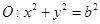 过
过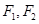 ,且
,且 的周长为
的周长为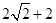 .
.
(Ⅰ)求椭圆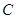 和圆
和圆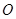 的方程;
的方程;
(Ⅱ)若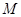 为圆
为圆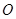 上任意一点,设直线
上任意一点,设直线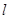 的方程为:
的方程为: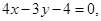 求
求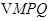 面积
面积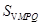 的最大值.
的最大值.
(本小题满分13分)已知函数
(1)若函数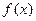 的反函数是其本身,求
的反函数是其本身,求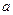 的值;
的值;
(2)当 时,求函数
时,求函数 的最大值.
的最大值.
(本小题满分13分)设数列 为等差数列,
为等差数列, 为
为 的前
的前 项和,已知
项和,已知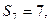
 ,
,
(1)求首项 和公差
和公差 ;
;
(2) 为数列
为数列 的前
的前 项的和,求
项的和,求 .
.
已知函数 ,
,
(1)求函数 的极值;
的极值;
(2)讨论函数 在区间
在区间 上的最大值.
上的最大值.
某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资
成正比,其关系如图1,B产品的利润与投资的算术平方根成 正比,其关系如图2(注:利
正比,其关系如图2(注:利
润与投资单位是万元)
(1)分别将A,B两种产 品的利润表示为投资的函数,并写
品的利润表示为投资的函数,并写 出它们的函数关系式.
出它们的函数关系式.
(2)该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10
万元投资,才能是企业获得最大利润,其最大利润约为多少万元(精确到1万元)?.

已知函数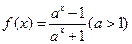 .
.
(1)判断函数的奇偶性;
(2)求该函数的值域;
(3)证明 是
是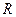 上的增函数.
上的增函数.