(本小题满分14分)如图,已知四面体ABCD的四个面均为锐角三角形,E、F、G、H分别为边AB、BC、CD、DA上的点,BD∥平面EFGH,且EH=FG.
(1) 求证:HG∥平面ABC;
(2) 请在面ABD内过点E作一条线段垂直于AC,并给出证明.
已知函数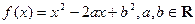 .
.
(1)若从集合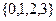 中任取一个元素
中任取一个元素 ,从集合
,从集合 中任取一个元素
中任取一个元素 ,求方程
,求方程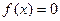 有两个不相等实根的概率;
有两个不相等实根的概率;
(2)若 是从区间
是从区间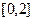 中任取的一个数,
中任取的一个数, 是从区间
是从区间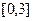 中任取的一个数,求方程
中任取的一个数,求方程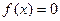 没有实根的概率.
没有实根的概率.
已知函数 ,其中
,其中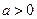 .
.
(1)若 在
在 处取得极值,求
处取得极值,求 的值;
的值;
(2)求 的单调区间;
的单调区间;
(3)若 的最小值为1,求
的最小值为1,求 的取值范围.
的取值范围.
已知 是椭圆
是椭圆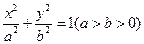 的左、右焦点,过点
的左、右焦点,过点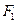 作
作
倾斜角为 的动直线
的动直线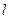 交椭圆于
交椭圆于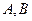 两点.当
两点.当 时,
时, ,且
,且 .
.
(1)求椭圆的离心率及椭圆的标准方程;
(2)求△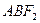 面积的最大值,并求出使面积达到最大值时直线
面积的最大值,并求出使面积达到最大值时直线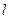 的方程.
的方程.
已知函数 .
.
(1)解关于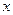 的不等式
的不等式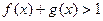 ;
;
(2)若对
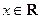 ,
,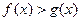 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知直线 的参数方程为
的参数方程为 (t为参数),曲线C的极坐标方程是
(t为参数),曲线C的极坐标方程是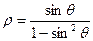 以极点为原点,极轴为x轴正方向建立直角坐标系,点
以极点为原点,极轴为x轴正方向建立直角坐标系,点 ,直线
,直线 与曲
与曲
线C交于A,B两点.
(1)写出直线 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
(2)线段MA,MB长度分别记|MA|,|MB|,求|MA|·|MB|的值.