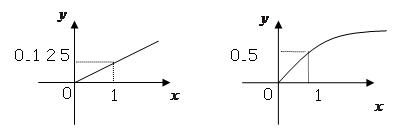.(本小题满分14分)
已知数列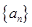 ,
,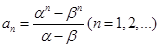 ,其中
,其中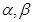 是方程
是方程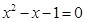 的两个根.
的两个根.
(1)证明:对任意正整数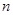 ,都有
,都有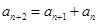 ;
;
(2)若数列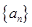 中的项都是正整数,试证明:任意相邻两项的最大公约数均为1;
中的项都是正整数,试证明:任意相邻两项的最大公约数均为1;
(3)若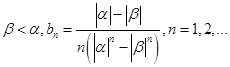 ,证明:
,证明: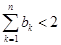 。
。
如图,在直三棱柱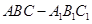 中,
中, 、
、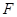 分别是
分别是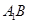 、
、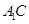 的中点,点
的中点,点 在
在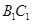 上,
上,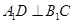 。
。 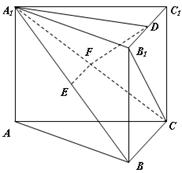
求证:(1)EF∥平面ABC;
(2)平面
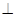 平面
平面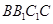 .
.
已知圆C过点(1,0),且圆心在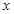 轴的正半轴上,直线l:y=x-1被该圆所截得的弦长为2
轴的正半轴上,直线l:y=x-1被该圆所截得的弦长为2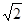 ,求圆C的标准方程.
,求圆C的标准方程.
高等数学中经常用到符号函数,符号函数的定义为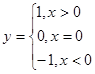 ,试编写算法,画出流程图,写出程序输入x的值,输出y的值。
,试编写算法,画出流程图,写出程序输入x的值,输出y的值。
已知函数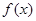 的定义域关于原点对称,且满足以下三个条件:
的定义域关于原点对称,且满足以下三个条件:
①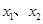 、
、 是定义域中的数时,有
是定义域中的数时,有 ;
;
②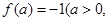
 是定义域中的一个数);
是定义域中的一个数);
③当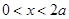 时,
时,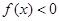 .
.
(1)判断 与
与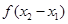 之间的关系,并推断函数
之间的关系,并推断函数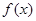 的奇偶性;
的奇偶性;
(2)判断函数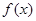 在
在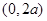 上的单调性,并证明;
上的单调性,并证明;
(3)当函数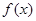 的定义域为
的定义域为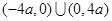 时,
时,
①求 的值;②求不等式
的值;②求不等式 的解集.
的解集.
某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).
(1)分别写出两种产品的收益与投资额的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?