某家庭进行理财投资，根据长期收益率市场预测，投资债券等稳健型产品的收益与投资额成正比，投资股票等风险型产品的收益与投资额的算术平方根成正比．已知投资1万元时两类产品的收益分别为0．125万元和0．5万元（如图）．
（1）分别写出两种产品的收益与投资额的函数关系；
（2）该家庭现有20万元资金，全部用于理财投资，问：怎么分配资金能使投资获得最大收益，其最大收益是多少万元？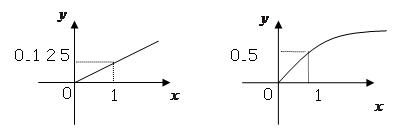
求椭圆
=1(a>b>0)的内接矩形面积的最大值.
设椭圆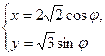
(φ为参数)上一点M与原点的连线与x轴正方向所成角为
,求点M的坐标.
已知中心在原点,对称轴为坐标轴的椭圆与直线x+y=3相交于A、B两点,C是AB的中点,若|AB|=2
,O是坐标原点,OC的斜率为2,求椭圆的方程.
设椭圆
=1的焦点为F1、F2,P是椭圆上任意一点,一条斜率为
的直线交椭圆于A、B两点,如果当a变化时,总可同时满足:
①∠F1PF2的最大值为
;
②直线l:ax+y+1=0平分线段AB.
求a的取值范围.
以椭圆
+y2=1(a>1)短轴的一个端点B(0,1)为直角顶点作椭圆的内接等腰直角三角形,问这样的直角三角形是否存在?如果存在,请说明理由,并判断最多能作出几个这样的三角形;如果不存在,请说明理由.