.(本小题满分14分)
已知椭圆 、抛物线
、抛物线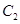 的焦点均在
的焦点均在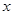 轴上,
轴上, 的中心和
的中心和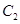 的顶点均为原点
的顶点均为原点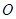 ,从每条曲
,从每条曲
线上取两个点,将其坐标记录于下表中:
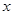 |
3 |
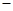 2 2 |
4 |
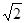 |
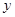 |
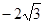 |
0 |
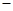 4 4 |
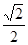 |
(Ⅰ)求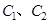 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线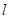 满足条件:①过
满足条件:①过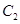 的焦点
的焦点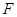 ;②与
;②与 交不同两点
交不同两点 且满
且满
足 ?若存在,求出直线
?若存在,求出直线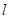 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
(本大题8分)已知正方体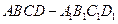 ,求:
,求:
(1)异面直线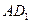 与
与 所成的角;
所成的角;
(2)证明:直线 //平面
//平面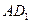 C
C
(3)二面角D— A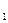 B—C
B—C 的大小;
的大小;
(本大题8分)
在空间直角坐标系中,已知A(3,0,1)和B(1,0,-3),试问
(1)在y轴上是否存在点M,满足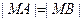 ?
?
(2)在y轴上是否存在点M,使△MAB为等边三角形?若存在,试求出点M坐标.
(本大题8分)
命题 方程
方程 有两个不等的正实数根,命题
有两个不等的正实数根,命题 方程
方程 无实数根。若“
无实数根。若“ 或
或 ”为真命题,求
”为真命题,求 的取值范围。
的取值范围。
已知圆 与直线
与直线 相交于P、Q两点,O为原点,且
相交于P、Q两点,O为原点,且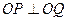 ,求实数
,求实数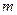 的值。
的值。
如图,四边形ABCD是正方形,MA⊥平面ABCD,MA∥PB,PB=AB= =
=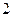

(1)求证: DM∥面PBC;
(2)求证:面PBD⊥面PAC;