为了解学生身高情况，某校以10%的比例对全校700名学生按性-优题课

题文

为了解学生身高情况，某校以10%的比例对全校700名学生按性别进行抽样检查，测得身高情况的统计图如图所示：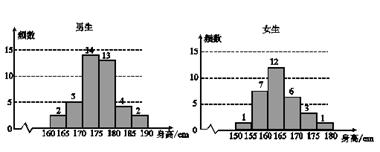

(1)估计该校男生的人数；
(2)估计该校学生身高在170～185cm的概率；
(3)从样本中身高在180～190cm的男生中任选2人，求至少有1人身高在185～190cm的概率．

科目数学题型解答题难度中等

知识点：误差估计

登录免费查看答案和解析

相关试题

如图，圆柱 $O O_{1}$ 内有一个三棱柱 $A B C - A_{1} B_{1} C_{1}$ ，三棱柱的底面为圆柱底面的内接三角形，且 $A B$ 是圆 $O$ 的直径。

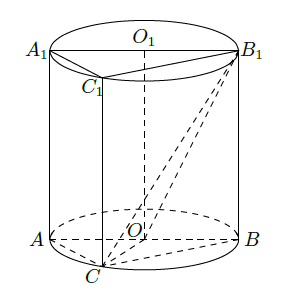
（Ⅰ）证明：平面 $A_{1} A C C_{1} ⊥ 平面 B_{1} B C C_{1}$ ；
（Ⅱ）设 $A B = A A_{1}$ 。在圆柱 $O O_{1}$ 内随机选取一点，记该点取自于三棱柱 $A B C - A_{1} B_{1} C_{1}$ 内的概率为 $P$ 。
（i）当点 $C$ 在圆周上运动时，求 $P$ 的最大值；
(ii)记平面 $A_{1} A C C_{1}$ 与平面 $B_{1} O C$ 所成的角为 $θ (0^{°} < θ \leq 90^{°})$ 。当 $P$ 取最大值时，求 $\cos θ$ 的值。

已知中心在坐标原点 $O$ 的椭圆 $C$ 经过点 $A (2, 3)$ ，且点 $F (2, 0)$ 为其右焦点。
（Ⅰ）求椭圆 $C$ 的方程；

（Ⅱ）是否存在平行于 $O A$ 的直线 $L$ ，使得直线 $L$ 与椭圆 $C$ 有公共点，且直线 $O A$ 与 $L$ 的距离等于4？若存在，求出直线 $L$ 的方程；若不存在，说明理由。

设 $S$ 是不等式 $x^{2} - x - 6 \leq 0$ 的解集，整数 $m, n \in S$ 。
（Ⅰ）记"使得 $m + n = 0$ 成立的有序数组 $(m, n)$ "为事件 $A$ ，试列举 $A$ 包含的基本事件；
（Ⅱ）设 $ξ = m^{2}$ ,求 $ξ$ 的分布列及其数学期望 $E ξ$ 。

已知△ABC的三边长为有理数
（1）求证cosA是有理数；（2）对任意正整数n，求证cosnA也是有理数

某厂生产甲、乙两种产品，生产甲产品一等品80%，二等品20%；生产乙产品，一等品90%，二等品10%。生产一件甲产品，如果是一等品可获利4万元，若是二等品则要亏损1万元；生产一件乙产品，如果是一等品可获利6万元，若是二等品则要亏损2万元。设生产各种产品相互独立
（1）记x（单位：万元）为生产1件甲产品和件乙产品可获得的总利润，求x的分布列
（2）求生产4件甲产品所获得的利润不少于10万元的概率

试卷网试题网古诗词网作文网范文网