.汽车从A地开往B地,如果在原计划时间的前一半时间每小时驶40千米,而后一半时间由每小时行驶50千米,可按时到达.但汽车以每小时40千米的速度行至离AB中点还差40千米时发生故障,停车半小时后,又以每小时55千米的速度前进,结果仍按时到达B地.求AB两地的距离及原计划行驶的时间.
已知二次函数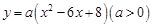 的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.
的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.
(1)如图①,连接AC,将△OAC沿直线AC翻折,若点O的对应点O'恰好落在该抛物线的对称轴上,求实数a的值;
(2)如图②,在正方形EFGH中,点E、F的坐标分别是(4,4)、(4,3),边HG位于边EF的右侧.若点P是边EF或边FG上的任意一点,求证四条线段PA、PB、PC、PD不能构成平行四边形;
(3)如图②,正方形EFGH向左平移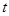 个单位长度时,正方形EFGH上是否存在一点P(包括正方形的边界),使得四条线段PA、PB、PC、PD能够构成平行四边形?如果存在,请求出
个单位长度时,正方形EFGH上是否存在一点P(包括正方形的边界),使得四条线段PA、PB、PC、PD能够构成平行四边形?如果存在,请求出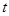 的取值范围.
的取值范围.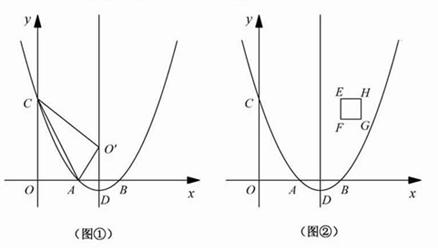
十一届全国人大常委会第二十次会议审议的个人所得税法修正案草案 (简称“个税法草案”),拟将现行个人所得税的起征点由每月2000元提高到3000元,并将9级超额累进税率修改为7级,两种征税方法的1~5级税率情况见下表:
| 税级 |
现行征税方法 |
草案征税方法 |
||||
| 月应纳税额x |
税率 |
速算扣除数 |
月应纳税额x |
税率 |
速算扣除数 |
|
| 1 |
x≤500 |
5% |
0 |
x≤1 500 |
5% |
0 |
| 2 |
500<x≤2000 |
10% |
25 |
1500<x≤4500 |
10% |
▲ |
| 3 |
2000<x≤5000 |
15% |
125 |
4500<x≤9000 |
20% |
▲ |
| 4 |
5000<x≤20000 |
20% |
375 |
9000<x≤35000 |
25% |
975 |
| 5 |
20000<x≤40000 |
25% |
1375 |
35000<x≤55 000 |
30% |
2725 |
注:“月应纳税额”为个人每月收入中超出起征点应该纳税部分的金额.
“速算扣除数”是为快捷简便计算个人所得税而设定的一个数.
例如:按现行个人所得税法的规定,某人今年3月的应纳税额为2600元,他应缴税款可以用下面两种方法之一来计算:
方法一:按1~3级超额累进税率计算,即500×5%+1500×10%十600×15%=265(元).
方法二:用“月应纳税额x适用税率一速算扣除数”计算,即2600×15%一l25=265(元)。
(1)请把表中空缺的“速算扣除数”填写完整;
(2)甲今年3月缴了个人所得税1060元,若按“个税法草案”计算,则他应缴税款多少元?
(3)乙今年3月缴了个人所得税3千多元,若按“个税法草案”计算,他应缴的税款恰好不变,那么乙今年3月所缴税款的具体数额为多少元?
操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的圆形纸片进行如下设计:
纸片利用率= ×100%
×100%
发现:(1)方案一中的点A、B恰好为该圆一直径的两个端点.
你认为小明的这个发现是否正确,请说明理由.
(2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.
请帮忙计算方案二的利用率,并写出求解过程.
探究:(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.

“校园手机”现象越来越受到社会的关注.某校对本校若干名同学家长对“禁止中学生带手机到学校”现象的看法进行调查,根据调查的数据绘制成如下的条形统计图和扇形统计图.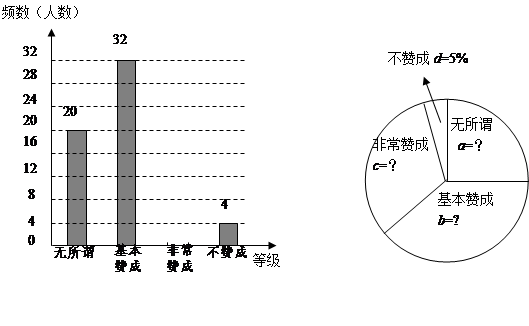
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)该校共抽查了__________名同学的体育测试成绩,扇形统计图中A、B、C级所占的百分比分别为a=___________;b= ___________;c=_________;
(2)补全条形统计图;
(3)若该校同学共有1600名同学,请你估计该校同学家长认同孩子带手机有___________人.请你谈谈对这个调查结果的看法.
已知线段OA⊥OB,C为OB上中点,D为AO上一点,连AC、BD交于P点.
(1)如图1,当OA=OB且D为AO中点时,求 的值;
的值;
(2)如图2,当OA=OB, =
= 时,求△BPC与△ACO的面积之比.
时,求△BPC与△ACO的面积之比.