某电视 台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,
台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,
相关的数据如下表所示:
| |
文艺节目 |
新闻节目 |
总计 |
| 20至40岁 |
40 |
18 |
58 |
| 大于40岁 |
15 |
27 |
42 |
| 总计 |
55 |
45 |
100 |
(1)由表中数据直观分析,收看新闻节目的观众是否与年龄有关?
(2)用分层抽样方法从收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(3)从上述5名观众中任取2名,求恰有1名在20至40岁之间的概率
如图1,在四棱锥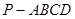 中,
中,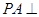 底面
底面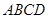 ,面
,面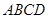 为正方形,
为正方形,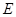 为侧棱
为侧棱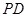 上一点,
上一点,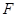 为
为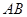 上一点.该四棱锥的正(主)视图和侧(左)视图如图2所示.
上一点.该四棱锥的正(主)视图和侧(左)视图如图2所示.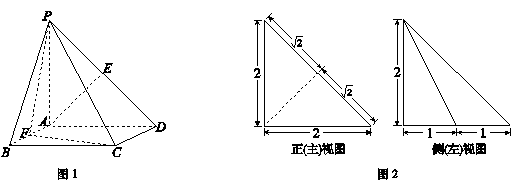
(Ⅰ)求四面体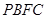 的体积;
的体积;
(Ⅱ)证明: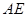 ∥平面
∥平面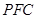 ;
;
(Ⅲ)证明:平面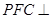 平面
平面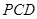 .
.
如图,在直角坐标系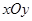 中,角
中,角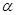 的顶点是原点,始边与
的顶点是原点,始边与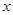 轴正半轴重合,终边交单位圆于点
轴正半轴重合,终边交单位圆于点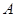 ,且
,且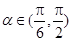 .将角
.将角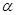 的终边按逆时针方向旋转
的终边按逆时针方向旋转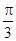 ,交单位圆于点
,交单位圆于点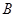 .记
.记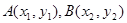 .
.
(Ⅰ)若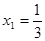 ,求
,求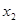 ;
;
(Ⅱ)分别过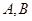 作
作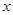 轴的垂线,垂足依次为
轴的垂线,垂足依次为 .记△
.记△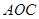 的面积为
的面积为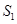 ,△
,△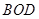 的面积为
的面积为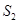 .若
.若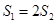 ,求角
,求角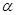 的值.
的值.
已知等比数列 的各项均为正数,
的各项均为正数,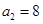 ,
,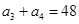 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设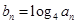 .证明:
.证明: 为等差数列,并求
为等差数列,并求 的前
的前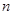 项和
项和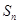 .
.
设函数
(Ⅰ)解不等式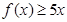 ;
;
(Ⅱ)若函数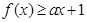 的解集为
的解集为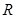 ,求实数
,求实数 的取值范围
的取值范围
在极坐标系中,已知圆 的圆心
的圆心 ,半径
,半径
(Ⅰ)求圆 的极坐标方程;
的极坐标方程;
(Ⅱ)若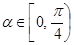 ,直线
,直线 的参数方程为
的参数方程为 (
( 为参数),直线
为参数),直线 交圆
交圆 于
于 两点,求弦长
两点,求弦长 的取值范围
的取值范围