设函数 .
.
(1)确定函数f (x)的定义域;
(2)判断函数f (x)的奇偶性;
(3)证明函数f (x)在其定义域上是单调增函数;
已知函数 ,其中
,其中 .
.
(1)若 ,求函数
,求函数 的极值;
的极值;
(2)当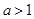 时,试确定函数
时,试确定函数 的单调区间.
的单调区间.
如图,在三棱锥 中,
中, 底面
底面 ,
, ,
, 为
为 的中点,
的中点, 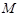 为
为 的中点,
的中点, ,
,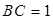 .
.
(1)求证: 平面
平面 ;
;
(2)求 与平面
与平面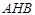 成角的正弦值;
成角的正弦值;
(3)设点 在线段
在线段 上,且
上,且 ,
, 平面
平面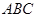 ,求实数
,求实数 的值.
的值.
为了解某校学生的视力情况,现采用随机抽样的方式从该校的A,B两班中各抽5名学生进行视力检测.检测的数据如下:
A班5名学生的视力检测结果:4.3,5.1,4.6,4.1,4.9.
B班5名学生的视力检测结果:5.1,4.9,4.0,4.0,4.5.
(1)分别计算两组数据的平均数,从计算结果看,哪个班的学生视力较好?
(2)由数据判断哪个班的5名学生视力方差较大?(结论不要求证明)
(3)现从A班的上述5名学生中随机选取3名学生,用X表示其中视力大于4.6的人数,求X的分布列和数学期望.
在平面直角坐标系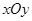 中,点
中,点 ,
,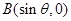 ,其中
,其中 .
.
(1)当 时,求向量
时,求向量 的坐标;
的坐标;
(2)当 时,求
时,求 的最大值.
的最大值.
给定数列
(1)判断 是否为有理数,证明你的结论;
是否为有理数,证明你的结论;
(2)是否存在常数 .使
.使 对
对 都成立? 若存在,找出
都成立? 若存在,找出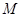 的一个值, 并加以证明; 若不存在,说明理由.
的一个值, 并加以证明; 若不存在,说明理由.