一位同学拿了两块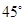 三角尺
三角尺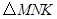 ,
,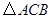 做了一个探究活动:将
做了一个探究活动:将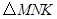 的直角顶点
的直角顶点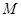 放在
放在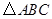 的斜边
的斜边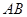 的中点处,设
的中点处,设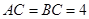 .
. 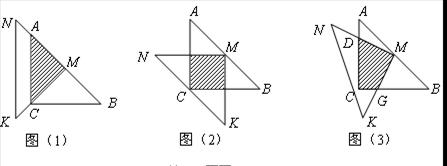
(1)如图(1),两三角尺的重叠部分为
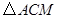 ,则重叠部分的面积为 ,周长为
,则重叠部分的面积为 ,周长为  .
. (2)将图(1)中的
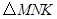 绕顶点
绕顶点 逆时针旋转
逆时针旋转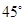 ,得到图26(2),此时重叠部分的面积为 ,周长为 .
,得到图26(2),此时重叠部分的面积为 ,周长为 . (3)如果将
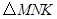 绕
绕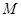 旋转到不同于图(1)和图(2)的图形,如图(3)
旋转到不同于图(1)和图(2)的图形,如图(3) ,请你猜想此时重叠部分的面积为 .
,请你猜想此时重叠部分的面积为 . (4)在图(3)情况下,若
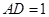 ,求出重叠部分图形的周长.
,求出重叠部分图形的周长.
如图,在△ABC中,D为AC边的中点,且DB⊥BC,BC=4,CD=5.
(1)求DB的长;
(2)在△ABC中,求BC边上高的长.
如图,小黄和小陈观察蜗牛爬行,蜗牛在以A为起点沿直线匀速爬向B点的过程中,到达C点时用了6分钟,那么还需要多长时间才能到达B点?
计算: .
.
在矩形ABCD中,AB=a,AD=b,点M为BC边上一动点(点M与点B、C不重合),连接AM,过点M作MN⊥AM,垂足为M,MN交CD或CD的延长线于点N.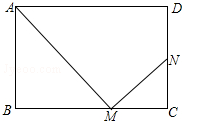
(1)求证:△CMN∽△BAM;
(2)设BM=x,CN=y,求y关于x的函数解析式.当x取何值时,y有最大值,并求出y的最大值;
(3)当点M在BC上运动时,求使得下列两个条件都成立的b的取值范围:①点N始终在线段CD上,②点M在某一位置时,点N恰好与点D重合.
已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC交⊙O于点D,交AC于点E,连接AD、BD,BD交AC于点F.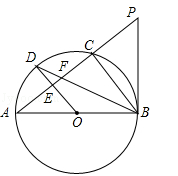
(1)求证:BD平分∠ABC;
(2)延长AC到点P,使PF=PB,求证:PB是⊙O的切线;
(3)如果AB=10,cos∠ABC=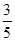 ,求AD.
,求AD.