已知定义在R上的奇函数 f(x)有最小正周期2,且当x∈(0,1)时, f(x)= .
.
(1) 求 f(x)在[-1,1]上的解析式;
(2) 证明: f(x)在(0,1)上是减函数.
设甲、乙、丙三个乒乓球协会的运动员人数分别为27,9,18,先采用分层抽样的方法从这三个协会中抽取6名运动员参加比赛.
(I)求应从这三个协会中分别抽取的运动员人数;
(II)将抽取的6名运动员进行编号,编号分别为 ,从这6名运动员中随机抽取2名参加双打比赛.
,从这6名运动员中随机抽取2名参加双打比赛.
(i)用所给编号列出所有可能的结果;
(ii)设A为事件“编号为 的两名运动员至少有一人被抽到”,求事件A发生的概率.
的两名运动员至少有一人被抽到”,求事件A发生的概率.
已知函数
(Ⅰ)求 最小正周期;
最小正周期;
(Ⅱ)求 在区间
在区间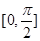 上的最大值和最小值.
上的最大值和最小值.
已知椭圆 (
(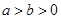 )上的点P到左、右两焦点
)上的点P到左、右两焦点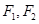 的距离之和为
的距离之和为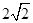 ,离心率为
,离心率为 .
.
(1)求椭圆的方程;
过右焦点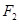 的直线
的直线 交椭圆于A、B两点.
交椭圆于A、B两点.
若y轴上一点 满足
满足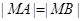 ,求直线
,求直线 斜率k的值;
斜率k的值;
(2)是否存在这样的直线 ,使
,使 的最大值为
的最大值为 (其中O为坐标原点)?若存在,求直线
(其中O为坐标原点)?若存在,求直线 方程;若不存在,说明理由.
方程;若不存在,说明理由.
小王于年初用50万元购买一辆大货车,第一年因缴纳各种费用支出6万元,从第二年起,每年都比上一年增加支出2万元,假定该年每年的运输收入均为25万元,小王在该车运输累计收入超过总支出后,考虑将大货车作为二手车出售,若该车在第 年年底出售,其销售价格为
年年底出售,其销售价格为 万元(国家规定大货车的报废年限为10年).
万元(国家规定大货车的报废年限为10年).
(1)大货车运输到第几年底,该车运输累计收入超过总支出?
(2)在第几年年底将大货车出售,能使小王获得的年平均利润最大?(利润=运输累计收入+销售收入-总支出)
在平面直角坐标系中,已知点 ,点B在直线
,点B在直线 上运动,过点B与
上运动,过点B与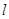 垂直的直线和线段AB的垂直平分线相交于点M.
垂直的直线和线段AB的垂直平分线相交于点M.
(1)求动点M的轨迹E的方程;
(2)过(1)中轨迹E上的点 作轨迹E的切线,求切线方程.
作轨迹E的切线,求切线方程.