如图,在坐标系中,菱形ABCD的边BC与x轴重合,点B与原点重合,AB=10, ∠ABC=60°.动点P从点B出发沿BC边以每秒1个单位长的速度匀速运动;动点Q从点D出发沿折线DC-CB-BA以每秒3个单位长的速度匀速运动,过点P作PF⊥BC,交折线AB-AC于点E,交直线AD于点F.若P、Q两点同时出发,当其中一点到达终点时整个运 动随之停止,设运动时间为
动随之停止,设运动时间为 t秒.
t秒.
(1)写出点A与点D的坐标
(2)当t=3秒时,试判断QE与AB之间的位置关系?
(3)当Q在线段DC上运动时,若△PQF为等腰三角形,求t的值;
(4)设△PQE的面积为S,求S与t的函数关系式;
已知两个全等的直角三角形纸片ABC、DEF,如图(1)放置,点B、D重合,点F在BC上,AB与EF交于点G、∠C=∠EFB=90°,∠E=∠ABC=30°,AB=DE=4.
(1)求证:△EGB是等腰三角形
(2)若纸片DEF不动,问△ABC绕点F逆时针旋转最小度时,四边形ACDE成为以ED为底的梯形(如图(2))求此梯形的高.
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2=(1+)2,善于思考的小明进行了以下探索:
设a+b=(m+n)2(其中a、b、m、n均为整数),
则有a+b=m2+2n2+2mn.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把部分a+b的式子化为平方 式的方法.
请仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b=(m+n)2,用含m、n的式子分别表示a、b,得a=_,b=_;
(2)利用所探索的结论,找一组正整数a、b、m、n,
填空:_+_=(_+_)2;
(3)若a+4=(m+n)2,且a、m、n均为正整数,求a的值.
如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,且CF=CE.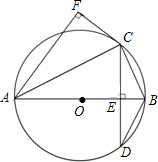
(1)求证:CF是⊙O的切线;
(2)若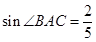 ,求
,求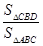 的值
的值
某企业2010年盈利1500万元,2012年克服金融危机的不利影响,仍实现盈利2160万元。从2010年到2012年,如果该企业每年的盈利的年增长率相同
求:(1)、该企业2011年盈利多少万元?
(2)、若该企业盈利的年增长率继续保持不变,预计2013年盈利多少万元?
为丰富学生的校园文化生活,珠海第十中学举办了“十中好声音”才艺比赛,三个年级都有男、女各一名选手进入决赛.初一年级选手编号为男1号、女1号,初二年级选手编号为男2号、女2号,初三年级选手编号为男3号、女3号.比赛规则是男、女各一名选手组成搭档展示才艺.
(1)用列举法说明所有可能出现搭挡的结果;
(2)求同一年级男、女选手组成搭档的概率;
(3)求高年级男选手与低年级女选手组成搭档的概率.