己知:二次函数y=ax2+bx+6(a≠0)与x轴交于A、B两点(点A在点B的左侧)点
A、点B的横坐标是一元二次方程x2-4x-12=0的两个根.
(1)请直接写出点A、点B的坐标.
(2)请求出该二次函数表达式及对称轴和顶点坐标.
(3)如图1,在二次函数对称轴上是否存在点P,使△APC的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
(4)如图2,连接AC、BC,点Q是线段0B上一个动点(点Q不与点0、B重合).过点Q作QD∥AC交BC于点D,设Q点坐标(m,0),当△CDQ面积S最大时,求m的值.
如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.
(1)求证:BE=CE;
(2)以点E为圆心,ED长为半径画弧,分别交BE,CE于点F,G.若BC=4,∠EBD=30°,求图中阴影部分(扇形)的面积.
某校为了解该校九年级学生对蓝球、乒乓球、羽毛球、足球四种球类运动项目的喜爱情况,对九年级部分学生进行了随机抽样调查,每名学生必须且只能选择最喜爱的一项运动项目上,将调查结果统计后绘制成如图两幅不完整的统计图,请根据图中的信息,回答下列问题:
(1)这次被抽查的学生有 60 人;请补全条形统计图;
(2)在统计图2中,“乒乓球”对应扇形的圆心角是 144 度;
(3)若该校九年级共有480名学生,估计该校九年级最喜欢足球的学生约有 48 人.
解不等式 ≥
≥ ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.
对某一个函数给出如下定义:若存在实数 ,对于任意的函数值
,对于任意的函数值 ,都满足
,都满足 ,则称这个函数是有界函数,在所有满足条件的
,则称这个函数是有界函数,在所有满足条件的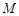 中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.
中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.
(1)分别判断函数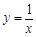
 和
和 是不是有界函数?若是有界函数,求其边界值;
是不是有界函数?若是有界函数,求其边界值;
(2)若函数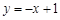
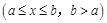 的边界值是2,且这个函数的最大值也是2,求
的边界值是2,且这个函数的最大值也是2,求 的取值范围;
的取值范围;
(3)将函数 的图象向下平移
的图象向下平移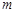 个单位,得到的函数的边界值是
个单位,得到的函数的边界值是 ,当
,当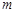 在什么范围时,满足
在什么范围时,满足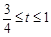 ?
?
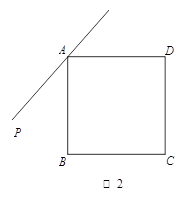
在正方形 外侧作直线
外侧作直线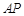 ,点
,点 关于直线
关于直线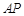 的对称点为
的对称点为 ,连接
,连接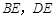 ,其中
,其中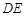 交直线
交直线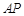 于点
于点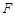 .
.
(1)依题意补全图1;
(2)若 ,求
,求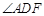 的度数;
的度数;
(3)如图2,若 ,用等式表示线段
,用等式表示线段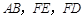 之间的数量关系,并证明.
之间的数量关系,并证明.