(1)解方程: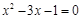 .
.
(2)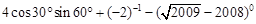
(本小题满分12分)在△ABC中,AB=AC,P是BC上任意一点.
(1)如图①,若P是BC边上任意一点,PF⊥AB于点F,PE⊥AC于点E,BD为△ABC的高线,试探求PE,PF与BD之间的数量关系;
(2)如图②,若P是BC延长线上一点,PF⊥AB于点F,PE⊥AC于点E,CD为△ABC的高线,试探求PE,PF与CD之间的数量关系.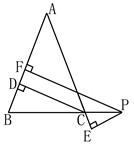
(本小题满分12分)如图1所示,已知在△ABC和△DEF中,AB=EF,∠B=∠E,EC=BD。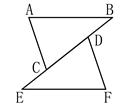
(1)试说明:△ABC≌△FED。
(2)若图形经过平移和旋转后得到图2,且有∠EDB=25º,∠A=66º,试求∠AMD的度数。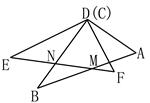
(3)将图形继续旋转后得到图3,此时D,B,F三点在同一条直线上,若DB=2DF,连接EB,已知△EFB的面积为5cm2,你能求出四边形ABED的面积吗?若能,请求出来;若不能,请你说明理由。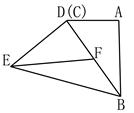
(本小题满分10分)如图,已知BD为△ABC的中线,CE⊥BD于E, AF⊥BD于F. 于是小白同学说:“BE+BF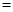 2BD ”.你认为他的判断对吗?为什么?
2BD ”.你认为他的判断对吗?为什么?
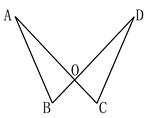
(本小题满分10分)如图,已知O是线段AC、DB的交点,且AC=BD,AB=DC.求证:OB=OC.