某校从参加高一年级期末考试的学生中抽出60名学生,并统计了他们的物理成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段[50,60),[60,70)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求出物理成绩低于50分的学生人数;
(2)估计这次考试物理学科及格率(60分及以上为及格)
已知函数 在点
在点 处取得极值。
处取得极值。
(1)求实数a的值;
(2)若关于x的方程 在区间[0,2]上有两个不等实根,求b的取值范围;
在区间[0,2]上有两个不等实根,求b的取值范围;
(3)证明:对于任意的正整数 ,不等式
,不等式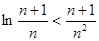 。
。
已知椭圆C的中心在坐标原点,焦点在x轴上,离心率为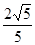 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线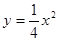 的焦点。
的焦点。
(1)求椭圆C的标准方程;
(2)过椭圆C的右焦点作直线l交椭圆C于A、B两点,交y轴于M点,若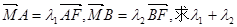 的值。
的值。
某研究小组在电脑上进行人工降雨摸拟试验,准备用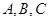 三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其试验数据统计如下:
三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其试验数据统计如下:
| 方式 |
实施地点 |
大雨 |
中雨 |
小雨 |
摸拟试验总次数 |
 |
甲 |
4次 |
6次 |
2次 |
12次 |
 |
乙 |
3次 |
6次 |
3次 |
12次 |
 |
丙 |
2次 |
2次 |
8次 |
12次 |
假设甲、乙、丙三地实施的人工降雨彼此互不影响.
(Ⅰ)求甲、乙两地恰为中雨且丙地为小雨的概率;
(Ⅱ)考虑到旱情和水土流失,如果甲地恰需中雨即能达到理想状态,乙地必须是大雨才能达到理想状态,丙地只要是小雨或中雨就能达到理想状态,求甲、乙、丙三地中至少有两地降雨量达到理想状态的概率.
如图,一张平行四边形的硬纸片 中,
中,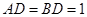 ,
, 。沿它的对角线
。沿它的对角线 把△
把△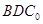 折起,使点
折起,使点 到达平面
到达平面 外点
外点 的位置。
的位置。
(Ⅰ)△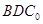 折起的过程中,判断平面
折起的过程中,判断平面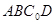 与平面
与平面 的位置关系,并给出证明;
的位置关系,并给出证明;
(Ⅱ)当△ 为等腰三角形,求此时二面角
为等腰三角形,求此时二面角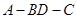 的大小。
的大小。
汶川震后在社会各界的支持和帮助下,汶川一中临时搭建了学校,学校餐厅也做到了保证每天供应1000名学生用餐,每星期一有A、B两样菜可供选择(每个学生都将从二者中选一),为了让学生们能够安心上课对学生的用餐情况进行了调查。调查资料表明,凡是在本周星期一选A菜的,下周星期一会有20%改选B,而选B菜的,下周星期一则有30%改选A,若用A 、B
、B 分别表示在第n个星期一选A、B菜的人数。
分别表示在第n个星期一选A、B菜的人数。
(1)试以A 表示A
表示A ;
;
(2)若A =200,求{A
=200,求{A }的通项公式;
}的通项公式;
(3)问第n个星期一时,选A与选B的人数相等?