已知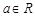 ,函数
,函数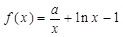 ,
,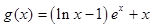 (其中
(其中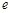 为自然对数的底数).(1)判断函数
为自然对数的底数).(1)判断函数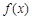 在
在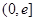 上的单调性;
上的单调性;
(2)是否存在实数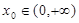 ,使曲线
,使曲线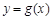 在点
在点 处的切线与
处的切线与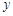 轴垂直? 若存在,
轴垂直? 若存在,
求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)若实数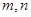 满足
满足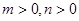 ,求证:
,求证: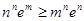 。
。
一种抛硬币游戏的规则是:抛掷一枚硬币,每次正面向上得1分,反面向上得2分.
(1)设抛掷5次的得分为ξ,求ξ的分布列和数学期望Eξ;
(2)求恰好得到n(n∈N*)分的概率.
如图,已知三棱柱ABC—A1B1C1的侧面与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N、P分别是CC1、BC、A1B1的中点.
(1)求证:PN⊥AM;
(2)若直线MB与平面PMN所成的角为θ,求sinθ的值.
选修45:不等式选讲
设x、y、z为正数,求证:2(x3+y3+z3)≥x2(y+z)+y2(x+z)+z2(x+y).
选修44:坐标系与参数方程
在平面直角坐标系xOy中,已知曲线C的参数方程为 (α为参数).以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(α为参数).以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 ,点P为曲线C上的动点,求点P到直线l距离的最大值.
,点P为曲线C上的动点,求点P到直线l距离的最大值.
选修42:矩阵与变换
已知矩阵M= 有特征值λ1=4及对应的一个特征向量e1=
有特征值λ1=4及对应的一个特征向量e1= .
.
(1)求矩阵M;
(2)求曲线5x2+8xy+4y2=1在M的作用下的新曲线的方程.