.(本小题满分14分)设抛物线 的方程为
的方程为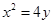 ,
,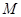 为直线
为直线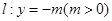 上任意一点,过点
上任意一点,过点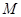 作抛物线
作抛物线 的两条切线
的两条切线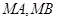 ,切点分别为
,切点分别为 ,
,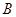 .
.
(1)当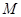 的坐标为
的坐标为 时,求过
时,求过 三点的圆的方程,并判断直线
三点的圆的方程,并判断直线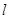 与此圆的位置关系;
与此圆的位置关系;
(2)求证:直线 恒过定点;
恒过定点;
(3)当 变化时,试探究直线
变化时,试探究直线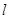 上是否存在点
上是否存在点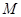 ,使
,使 为直角三角形,若存在,有几个这样的点,若不存在,说明理由.
为直角三角形,若存在,有几个这样的点,若不存在,说明理由.
设椭圆
 的右焦点为
的右焦点为 ,直线
,直线 与
与 轴交于点
轴交于点 ,若
,若 (其中
(其中 为坐标原点).
为坐标原点).
(1)求椭圆 的方程;
的方程;
(2)设 是椭圆
是椭圆 上的任意一点,
上的任意一点, 为圆
为圆 的任意一条直径(
的任意一条直径( 、
、 为直径的两个端点),求
为直径的两个端点),求 的最大值.
的最大值.
在直角梯形 中,
中, ,
,
 ,
, ,如图,把
,如图,把 沿
沿 翻折,使得平面
翻折,使得平面 平面
平面 .
.


(1)求证: ;
;
(2)若点 为线段
为线段 中点,求点
中点,求点 到平面
到平面 的距离;
的距离;
(3)在线段 上是否存在点
上是否存在点 ,使得
,使得 与平面
与平面 所成角为
所成角为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
某高中为了推进新课程改革,满足不同层次学生的需求,决定从高一年级开始,在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座。(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各学科讲座各天的满座的概率如下表: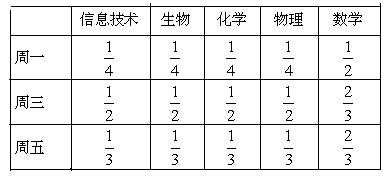
根据上表:
(1)求数学辅导讲座在周一、周三、周五都不满座的概率;
(2)设周三各辅导讲座满座的科目数为 ,求随机变量
,求随机变量 的分布列和数学期望。
的分布列和数学期望。
已知函数 (
( )的最小正周期为
)的最小正周期为 .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)将函数 的图象向左平移
的图象向左平移 个单位,再向上平移
个单位,再向上平移 个单位,得到函数
个单位,得到函数 的图象.若
的图象.若 在
在 上至少含有
上至少含有 个零点,求
个零点,求 的最小值.
的最小值.
已知函数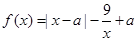 ,
, ,
,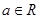 .
.
(1)若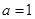 ,试判断并证明函数
,试判断并证明函数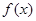 的单调性;
的单调性;
(2)当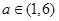 时,求函数
时,求函数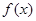 的最大值的表达式
的最大值的表达式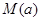 .
.