（本小题满分12分）
第4届湘台经贸洽谈交流会于2011年6月在我市举行，为了搞好接待工作，大会组委会在
某学院招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎
叶图（单位：cm）：若身高在175cm以上（包括175cm）定义为“高个子”，身高在175cm
以下（不包括175cm）定义为“ 非高个子”，且只有“女高个子”才担任“礼仪小姐”。（I）如
果用分层抽样的方法从“高个子”中和“非高个子”中提取5人，再从这5人中选2人，那么至
少有一人是“高个子”的概率是多少？（II）若从所有“高个子”中选3名志愿者，用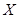
表示所
选志愿者中能担任“礼仪小姐”的人数，试写出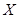的分布列，并求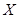的数学期望。
（本小题12分）已知函数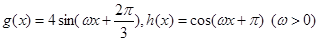
．
（Ⅰ）当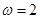
时，把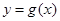
的图像向右平移
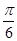个单位得到函数
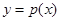的图像，求函数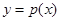的图像的对称中心坐标；
（Ⅱ）设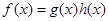
，若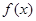
的图象与直线
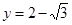的相邻两个交点之间的距离为π，求
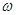的值，并求函数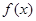的单调递增区间．
（本小题满分13分）已知椭圆
（
）经过点
，离心率为
，动点
（
）．
（1）求椭圆的标准方程；
（2）求以
（
为坐标原点）为直径且被直线
截得的弦长为
的圆的方程；
（3）设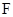
是椭圆的右焦点，过点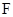作的垂线与以为直径的圆交于点
，证明线段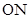
的长为定值，并求出这个定值．
已知等差数列
的公差不为零,
,等比数列
的前3项满足
．
（Ⅰ）求数列与的通项公式；
（Ⅱ）设
…
，是否存在最大整数
，使对任意的
，均有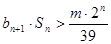
总成立?若存在,求出的值；若不存在,请说明理由
已知函数
处的切线l与直线
垂直，函数
（Ⅰ）求实数
的值；
（Ⅱ）若函数
存在单调递减区间，求实数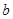
的取值范围；
（Ⅲ）设
是函数的两个极值点，若
，求
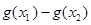的最小值．
某校高二年级的一次数学考试中，为了分析学生的得分情况，随机抽取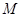
名同学的成绩，数据的分组统计表如下：
| 分组 |
频数 |
频率 |
频率/组距 |
| （40,50] |
2 |
0．02 |
0．002 |
| （50,60] |
4 |
0．04 |
0．004 |
| （60,70] |
11 |
0．11 |
0．011 |
| （70,80] |
38 |
0．38 |
0．038 |
| （80,90] |
 |
 |
 |
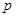| （90,100] |
11 |
0．11 |
0．011 |
| 合计 |
|
 |
 |
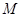（1）求出表中
的值；
（2）为了了解某些同学在数学学习中存在的问题，现从样本中分数在
中的6位同学中任意抽取2人进行调查，求分数在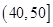
和
中各有一人的概率．