(本小题12分)已知函数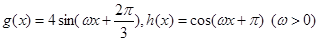 .
.
(Ⅰ)当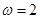 时,把
时,把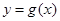 的图像向右平移
的图像向右平移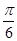 个单位得到函数
个单位得到函数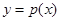 的图像,求函数
的图像,求函数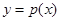 的图像的对称中心坐标;
的图像的对称中心坐标;
(Ⅱ)设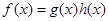 ,若
,若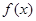 的图象与直线
的图象与直线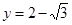 的相邻两个交点之间的距离为π,求
的相邻两个交点之间的距离为π,求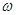 的值,并求函数
的值,并求函数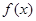 的单调递增区间.
的单调递增区间.
(本小题12分)已知函数 是定义在
是定义在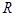 上的偶函数,已知
上的偶函数,已知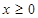 时,
时, .
.
(1)画出偶函数 的图象;
的图象;
(2)根据图象,写出 的单调区间;同时写出函数的值域.
的单调区间;同时写出函数的值域.
(本小题12分)已知函数 的定义域为集合A,
的定义域为集合A,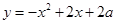 的值域为B.
的值域为B.
(1)若 ,求A∩B
,求A∩B
(2) 若 =R,求实数
=R,求实数 的取值范围。
的取值范围。
(本小题12分) 不用计算器求下列各式的值
⑴ 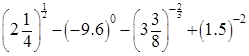
⑵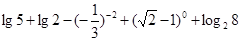
已知数列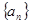 、
、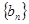 、
、 ,点
,点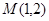 ,
,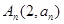 ,
,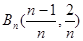 在一直线上。
在一直线上。
(1)求数列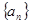 的通项公式;
的通项公式;
(2)若数列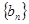 满足
满足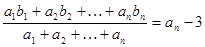 ,求数列
,求数列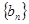 的通项公式;
的通项公式;
(3)若数列 的前
的前 项和为
项和为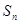 ,且满足
,且满足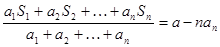 (
(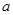 为常数),问点
为常数),问点 ,
,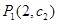 ,
, ,
,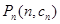 是否在同一直线上,请说明理由。
是否在同一直线上,请说明理由。
已知两定点 ,满足条件
,满足条件 的点
的点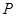 的轨迹是曲线
的轨迹是曲线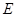 ,直线
,直线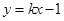 与曲线
与曲线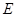 交于
交于 两点,如果
两点,如果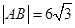 ,且曲线
,且曲线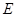 上存在点
上存在点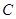 ,使
,使 .
.
(1)求曲线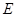 的方程;
的方程;
(2)求实数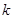 的值;
的值;
(3)求实数 的值。
的值。