如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,A1A=4,点D是BC的中点.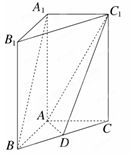
(1)求异面直线A1B与C1D所成角的余弦值;
(2)求平面ADC1与平面ABA1夹角的正弦值.
(12分)在平面直角坐标系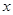 O
O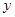 中,直线
中,直线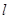 与抛物线
与抛物线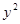 =2
=2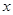 相交于A、B两点.
相交于A、B两点.
(Ⅰ)求证:命题“如果直线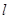 过点T(3,0),那么
过点T(3,0),那么 =3”是真命题;
=3”是真命题;
(Ⅱ)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
(12分)如图,已知三棱锥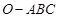 的侧棱
的侧棱 两两垂直,且
两两垂直,且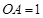 ,
, ,
,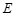 是
是 的中点.
的中点.
(Ⅰ)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(Ⅱ)BE和平面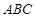 所成角的正弦值.
所成角的正弦值.
(12分) 如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且MD=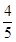 PD.
PD.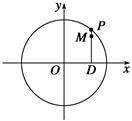
(Ⅰ)当P在圆上运动时,求点M的轨迹C的方程;
(Ⅱ)求过点(3,0)且斜率为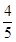 的直线被C所截线段的长度.
的直线被C所截线段的长度.
(12分)已知命题p:不等式 的解集为R,命题q:
的解集为R,命题q: 是R上的增函数,若p或q为真命题,p且q为假命题,求实数m的取值范围.
是R上的增函数,若p或q为真命题,p且q为假命题,求实数m的取值范围.
(理科题)(本小题12分)
某房产开发商投资81万元建一座写字楼,第一年装修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元。
(1)若扣除投资和各种装修费,则从第几年开始获取纯利润?
(2)若干年后开发商为了投资其他项目,有两种处理方案①年平均利润最大时以46万元出售该楼;
②纯利润总和最大时,以10万元出售楼,问选择哪种方案盈利更多?