(12分)如图,已知三棱锥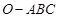 的侧棱
的侧棱 两两垂直,且
两两垂直,且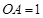 ,
, ,
,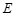 是
是 的中点.
的中点.
(Ⅰ)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(Ⅱ)BE和平面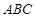 所成角的正弦值.
所成角的正弦值.
如图, ,
,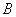 ,
,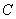 ,
,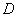 四点共圆,
四点共圆,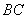 与
与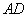 的延长线交于点
的延长线交于点 ,点
,点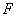 在
在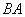 的延长线上.
的延长线上.
(1)若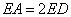 ,
, ,求
,求 的值;
的值;
(2)若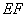 ∥
∥ ,求证:线段
,求证:线段 ,
,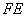 ,
, 成等比数列.
成等比数列.
已知函数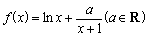 .
.
(1)当 时,求
时,求 的单调区间,如果函数
的单调区间,如果函数 仅有两个零点,求实数
仅有两个零点,求实数 的取值范围;
的取值范围;
(2)当 时,试比较
时,试比较 与1的大小.
与1的大小.
已知函数 (
(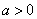 ,
,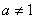 )的图象恒过定点
)的图象恒过定点 ,椭圆
,椭圆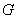 :
: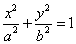 (
(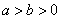 )的左,右焦点分别为
)的左,右焦点分别为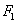 ,
, ,直线
,直线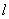 经过点
经过点 且与⊙
且与⊙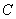 :
: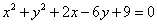 相切.
相切.
(1)求直线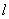 的方程;
的方程;
(2)若直线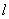 经过点
经过点 并与椭圆
并与椭圆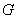 在
在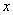 轴上方的交点为
轴上方的交点为 ,且
,且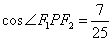 ,求
,求 内切圆的方程.
内切圆的方程.
如图,在正四棱锥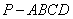 中,底面是边长为2的正方形,侧棱
中,底面是边长为2的正方形,侧棱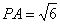 ,
,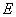 为
为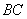 的中点,
的中点,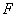 是侧棱
是侧棱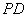 上的一动点。
上的一动点。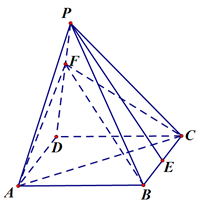
(1)证明: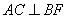 ;
;
(2)当直线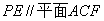 时,求三棱锥
时,求三棱锥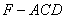 的体积.
的体积.
在一个盒子中,放有标号分别为 ,
,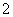 ,
, 的三个小球,现从这个盒子中,有放回地先后抽得两个小球的标号分别为
的三个小球,现从这个盒子中,有放回地先后抽得两个小球的标号分别为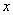 、
、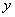 ,设
,设 为坐标原点,设
为坐标原点,设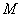 的坐标为
的坐标为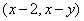 .
.
(1)求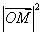 的所有取值之和;
的所有取值之和;
(2)求事件“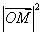 取得最大值”的概率.
取得最大值”的概率.