(本小题满分13分)已知椭圆 (
( )经过点
)经过点 ,离心率为
,离心率为 ,动点
,动点 (
( ).
).
(1)求椭圆的标准方程;
(2)求以 (
( 为坐标原点)为直径且被直线
为坐标原点)为直径且被直线 截得的弦长为
截得的弦长为 的圆的方程;
的圆的方程;
(3)设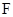 是椭圆的右焦点,过点
是椭圆的右焦点,过点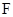 作
作 的垂线与以
的垂线与以 为直径的圆交于点
为直径的圆交于点 ,证明线段
,证明线段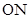 的长为定值,并求出这个定值.
的长为定值,并求出这个定值.
(本小题满分12分)下图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人
(Ⅰ)求该专业毕业总人数N和90~95分数段内的人数 ;
;
(Ⅱ)现欲将90~95分数段内的 名毕业生分配往甲、乙、丙三所学校,若向学校甲分配两名毕业生,且其中至少有一名男生的概率为
名毕业生分配往甲、乙、丙三所学校,若向学校甲分配两名毕业生,且其中至少有一名男生的概率为 ,求
,求 名毕业生中男女各几人(男女人数均至少两人)?
名毕业生中男女各几人(男女人数均至少两人)?
(Ⅲ)在(Ⅱ)的结论下,设随机变量 表示n名毕业生中分配往乙学校的三名学生中男生的人数,求
表示n名毕业生中分配往乙学校的三名学生中男生的人数,求 的分布列和数学期望.
的分布列和数学期望.
【改编】(本小题满分12分)在 中,角
中,角 所对的边为
所对的边为 ,且满足
,且满足
(1)求角 的值;
的值;
(2)若 且
且 ,求
,求 的取值范围.
的取值范围.
(本小题满分14分)已知函数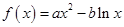 在点
在点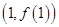 处的切线为
处的切线为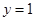 .
.
(1)求实数 ,
,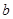 的值;
的值;
(2)是否存在实数 ,当
,当 时,函数
时,函数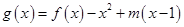 的最小值为
的最小值为 ,若存在,求出
,若存在,求出 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)若 ,求证:
,求证: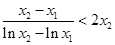 .
.
(本小题满分13分)已知抛物线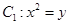 ,圆
,圆 .
.
(1)在抛物线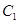 上取点
上取点 ,
,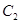 的圆周上取一点
的圆周上取一点 ,求
,求 的最小值;
的最小值;
(2)设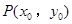
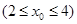 为抛物线
为抛物线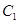 上的动点,过
上的动点,过 作圆
作圆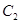 的两条切线,交抛物线
的两条切线,交抛物线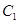 于
于 、
、 点,求
点,求 中点
中点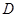 的横坐标的取值范围.
的横坐标的取值范围.
(本小题满分14分)已知首项为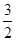 ,公比不等于
,公比不等于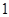 的等比数列
的等比数列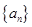 的前
的前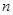 项和为
项和为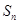 ,且
,且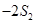 ,
, ,
, 成等差数列.
成等差数列.
(1)求数列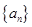 的通项公式;
的通项公式;
(2)令 ,数列
,数列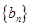 的前
的前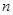 项和为
项和为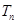 ,求证:
,求证:
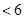 .
.