(本小题满分12分,(1)小问5分,(2)小分7分.)
如图所示,正三棱柱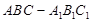 的底面边长与侧棱长均为
的底面边长与侧棱长均为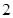 ,
, 为
为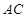 中点.
中点.
(1)求证: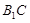 ∥平面
∥平面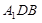 ;
;
(2)求直线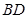 与平面
与平面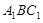 所成的角的正弦值.
所成的角的正弦值.
(本小题满分12分)设二次函数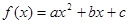 的图象过点(0,1)和(1,4),且对于任意的实数
的图象过点(0,1)和(1,4),且对于任意的实数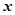 ,不等式
,不等式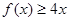 恒成立.
恒成立.
(Ⅰ)求函数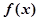 的表达式;
的表达式;
(Ⅱ)设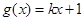 ,若
,若 在区间[1,2]上是增函数,求实数
在区间[1,2]上是增函数,求实数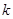 的取值范围.
的取值范围.
(本小题满分12分)某厂生产一种产品的固定成本(即固定投入)为0.5万元,但每生产一百件这样的产品,需要增加可变成本(即另增加投入)0.25万元. 市场对此产品的年需求量为500件,销售的收入函数为 (单位:万元),其中
(单位:万元),其中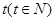 是产品售出的数量(单位:百件).
是产品售出的数量(单位:百件).
(Ⅰ)该公司这种产品的年产量为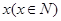 百件,生产并销售这种产品所得到的利润为当年产量
百件,生产并销售这种产品所得到的利润为当年产量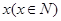
的函数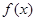 ,求
,求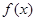 ;
;
(Ⅱ)当年产量是多少时,工厂所得利润最大?
(Ⅲ)当年产量是多少时, 工厂才不亏本?
(本小题满分12分)定义在R上的函数 满足:对任意实数
满足:对任意实数 ,总有
,总有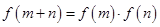 ,且当
,且当 时,
时,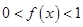 .
.
(Ⅰ)试求 的值;
的值;
(Ⅱ)判断 的单调性并证明你的结论.
的单调性并证明你的结论.
(本小题满分12分)已知指数函数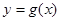 满足:
满足: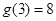 ,定义域为
,定义域为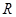 上的函数
上的函数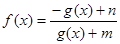 是奇函数.
是奇函数.
(Ⅰ)求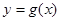 与
与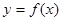 的解析式;
的解析式;
(Ⅱ)判断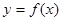 在
在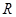 上的单调性并用单调性定义证明.
上的单调性并用单调性定义证明.
(本小题满分10分)已知全集U = R,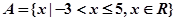 ,
,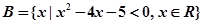 .
.
(Ⅰ)求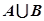 ;
;
(Ⅱ)求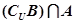 .
.