(本小题满分12分)设二次函数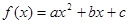 的图象过点(0,1)和(1,4),且对于任意的实数
的图象过点(0,1)和(1,4),且对于任意的实数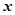 ,不等式
,不等式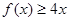 恒成立.
恒成立.
(Ⅰ)求函数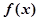 的表达式;
的表达式;
(Ⅱ)设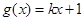 ,若
,若 在区间[1,2]上是增函数,求实数
在区间[1,2]上是增函数,求实数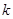 的取值范围.
的取值范围.
设集合 为方程
为方程 的解集,集合
的解集,集合 为方程
为方程 的解集,
的解集, ,求
,求 。
。
(1)若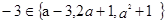 ,求实数
,求实数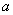 的值。
的值。
(2)计算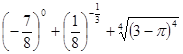
由下面四个图形中的点数分别给出了四个数列的前四项,将每个图形的层数增加可得到这四个数列的后继项.按图中多边形的边数依次称这些数列为“三角形数列”、“四边形数列” ,将构图边数增加到
,将构图边数增加到 可得到“
可得到“ 边形数列”,记它的第
边形数列”,记它的第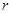 项为
项为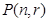 ,
,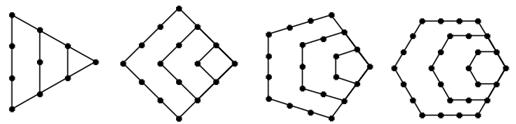
1,3,6,10 1,4,9,16 1,5,12,22 1,6,15,28
(1)求使得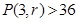 的最小
的最小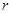 的取值;
的取值;
(2)试推导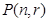 关于
关于 、
、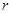 的解析式;
的解析式;
( 3)是否存在这样的“ 边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.
边形数列”,它的任意连续两项的和均为完全平方数,若存在,指出所有满足条件的数列并证明你的结论;若不存在,请说明理由.
已知函数 的图像(如图所示)过点
的图像(如图所示)过点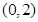 、
、 和点
和点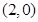 ,且函数图像关于点
,且函数图像关于点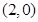 对称;直线
对称;直线 和
和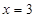 及
及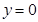 是它的渐近线.现要求根据给出的函数图像研究函数
是它的渐近线.现要求根据给出的函数图像研究函数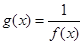 的相关性质与图像,
的相关性质与图像,
(1)写出函数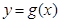 的定义域、值域及单调递增区间;
的定义域、值域及单调递增区间;
(2)作函数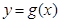 的大致图像(要充分反映由图像及条件给出的信息);
的大致图像(要充分反映由图像及条件给出的信息);
(3)试写出 的一个解析式,并简述选择这个式子的理由(按给出理由的完整性及表达式的合理、简洁程度分层给分
的一个解析式,并简述选择这个式子的理由(按给出理由的完整性及表达式的合理、简洁程度分层给分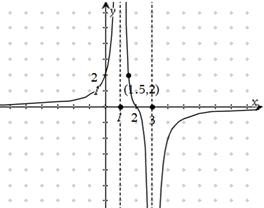
已知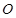 为坐标原点,点
为坐标原点,点 ,对于
,对于 有向量
有向量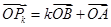 ,
,
(1)试问点 是否在同一条直线上,若是,求出该直线的方程;若不是,请说明理由;
是否在同一条直线上,若是,求出该直线的方程;若不是,请说明理由;
(2)是否在存在 使
使 在圆
在圆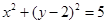 上或其内部,若存在求出
上或其内部,若存在求出 ,若不存在说明理由.
,若不存在说明理由.