计算机成本不断降低,若每隔 3 年计算机价格降低 ,现在价格为 8100 元的计算机,则 9 年后价格为多少元?
,现在价格为 8100 元的计算机,则 9 年后价格为多少元?
在 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为

(1)求角B;
(2)设 的取值范围。
的取值范围。
(本小题满分12分)已知点列M
 ,M
,M
 ,…,M
,…,M
 ,…,且
,…,且 与
与
 垂直,其中是不等于零的实常数,是正整数,设
垂直,其中是不等于零的实常数,是正整数,设 ,求数列
,求数列 的通项公式,并求其前n项和S
的通项公式,并求其前n项和S 。
。
如图所示,有两条相交成60°角的直路XX′和YY′,交点是O,甲、乙分别在OX、OY上,起初甲离O点3 km,乙离O点1 km,后来两人同时用每小时4 km的速度,甲沿XX′方向,乙沿Y′Y的方向步行.
(1)起初,两人的距离是多少?
(2)用t表示t小时后两人的距离;
(3)什么时候两人的距离最短?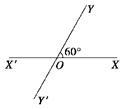
设△ABC的内角A,B,C的对边分别为a,b,c,且A=60°,c=3b.求:
(1)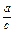 的值;
的值;
(2) 的值.
的值.
在△ABC中,设A、B、C的对边分别为a、b、c,向量m=(cosA,sinA),n=(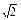 -sinA,cosA),若|m+n|=2.
-sinA,cosA),若|m+n|=2.
(1)求角A的大小;
(2)若b=4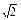 ,且c=
,且c=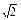 a,求△ABC的面积.
a,求△ABC的面积.