已知以点C (t, 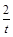 )(t∈R),t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.
)(t∈R),t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.
(1)求证:△OAB的面积为定值;
(2)设直线y= –2x+4与圆C交于点M,N若|OM|=|ON|,求圆C的方程.
(3)若t>0,当圆C的半径最小时,圆C上至少有三个不同的点到直线l:y –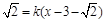 的距离为
的距离为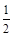 ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
已知椭圆 :
: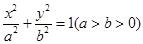 的离心率
的离心率 ,
,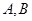 是椭圆
是椭圆 上两点,
上两点, 是线段
是线段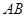 的中点,线段
的中点,线段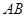 的垂直平分线与椭圆
的垂直平分线与椭圆 相交于
相交于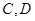 两点.
两点.
(1)求直线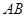 的方程;
的方程;
(2)是否存在这样的椭圆,使得以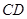 为直径的圆过原点
为直径的圆过原点 ?若存在,求出该椭圆方程;若不存在,请说明理由.
?若存在,求出该椭圆方程;若不存在,请说明理由.
如图,已知正三棱柱 的各棱长都是4,
的各棱长都是4,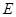 是
是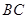 的中点,动点
的中点,动点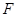 在线段
在线段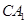 上,且不与点
上,且不与点 、
、 重合.
重合.
(1)若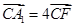 ,求平面
,求平面 与平面
与平面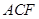 的夹角的余弦值;
的夹角的余弦值;
(2)求点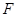 到直线
到直线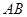 距离
距离 的最小值.
的最小值.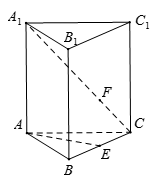
甲、乙两位同学各有3张卡片,现以投掷均匀硬币的形式进行游戏,当出现正面朝上时甲赢得乙一张卡片,否则乙赢得甲一张卡片.规定掷硬币的次数达6次时,或在此前某人已赢得所有卡片时游戏终止。设 表示游戏终止时掷硬币的次数。
表示游戏终止时掷硬币的次数。
(1)求第三次掷硬币后甲恰有4张卡片的概率;
(2)求 的分布列和数学期望
的分布列和数学期望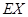 .
.
已知数列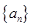 的前
的前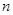 项和为
项和为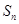 ,且满足:
,且满足: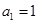 ,
,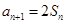 .
.
(1)求数列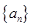 的通项公式;
的通项公式;
(2)设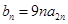 ,求数列
,求数列 的前
的前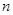 项和为
项和为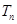 .
.
设函数 .
.
(1)求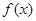 的最大值;
的最大值;
(2)求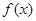 的对称中心;
的对称中心;
(3)将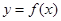 的图像按向量
的图像按向量 平移后得到的图象关于坐标原点对称,求长度最小的
平移后得到的图象关于坐标原点对称,求长度最小的 .
.