在数列{an}中,a1=1,当n≥2时,an,Sn,Sn-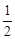 成等比数列.
成等比数列.
(1)求a2,a3,a4,并推出an的表达式;(2)用数学归纳法证明所得的结论;
(3)求数列{an}前n项的和.
已知a为实数,f(x)=(x2-4)(x-a).
(1)若f′(-1)=0,求f(x)在[-2,2]上的最大值和最小值;
(2)若f(x)在(-∞,-2]和[2,+∞)上都是递增的,求a的取值范围
已知函数f(x)=x2+ln x-1.
(1)求函数f(x)在区间[1,e](e为自然对数的底)上的最大值和最小值;
(2)求证:在区间(1,+∞)上,函数f(x)的图象在函数g(x)=x3的图象的下方
(3)(理)求证:[f′(x)]n-f′(xn)≥2n-2(n∈N*)
已知函数f=x++b,其中a,b∈R.
(1)若曲线y=f在点P处的切线方程为
y=3x+1,求函数f的解析式;
(2)讨论函数f的单调性;
(3)若对于任意的a∈,不等式f≤10在上恒成立,求b的取值范围.
如右图所示,已知A为抛物线C:y=2x2上的点,直线l1过点A,且
与抛物线C相切,直线l2:x=a交抛物线C于点B,交直线l1于点D.
(1)求直线l1的方程;
(2)求△ABD的面积S1.
(本小题满分16分)
对于函数y=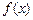 ,x∈(0,
,x∈(0,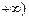 ,如果a,b,c是一个三角形的三边长,那么
,如果a,b,c是一个三角形的三边长,那么 ,
,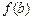 ,
, 也是一个三角形的三边长, 则称函数
也是一个三角形的三边长, 则称函数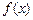 为“保三角形函数”.
为“保三角形函数”.
对于函数y=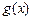 ,x∈
,x∈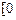 ,
,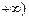 ,如果a,b,c是任意的非负实数,都有
,如果a,b,c是任意的非负实数,都有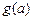 ,
, ,
,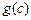 是一个三角形的三边长,则称函数
是一个三角形的三边长,则称函数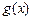 为“恒三角形函数”.
为“恒三角形函数”.
(1)判断三个函数“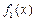 =x,
=x, =
=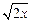 ,
, =
= (定义域均为x∈(0,
(定义域均为x∈(0,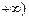 )”中,那些是“保三角形函数”?请说明理由;
)”中,那些是“保三角形函数”?请说明理由;
(2)若函数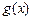 =
= ,x∈
,x∈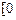 ,
,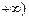 是“恒三角形函数”,试求实数k的取值范围;
是“恒三角形函数”,试求实数k的取值范围;
(3)如果函数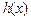 是定义在(0,
是定义在(0,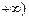 上的周期函数,且值域也为(0,
上的周期函数,且值域也为(0,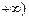 ,试证明:
,试证明: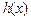 既不是“恒三角形函数”,也不是“保三角形函数”.
既不是“恒三角形函数”,也不是“保三角形函数”.