如图,直线y=x+2与抛物线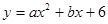 (a≠0)相交于A
(a≠0)相交于A 和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值,若存在,求出这个最大值;若不存在,请说明理由;
某商店准备进一批季节性小家电,单价40元.经市场预测,销售定价为52元时,可售出180个,定价每增加1元,销售量净减少10个;定价每减少1元,销售量净增加10个.因受库存的影响,每批次进货个数不得超过180个,商店若将准备获利2000元,则应进货多少个?定价为多少元?
如图,在平面直角坐标系中,⊙A的半径为1,圆心A点的坐标为(1,﹣2).直线OM是一次函数y=x的图像.让⊙A沿y轴正方向以每秒1个单位长度移动,移动时间为t.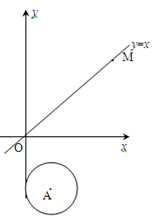
(1)填空
①直线OM与x轴所夹的锐角度数为°;
②当t=时,⊙A与坐标轴有两个公共点;
(2)当t>3时,求出运动过程中⊙A与直线OM相切时的t的值;
(3)运动过程中,当⊙A与直线OM相交所得的弦长为1时,求t的值.
如图,有两个可以自由转动的转盘A、B,转盘A被均匀分成4等份,每份标上1、2、3、4四个数字;转盘B被均匀分成6等份,每份标上1、2、3、4、5、6六个数字.有人为甲、乙两人设计了一个游戏,其规则如下: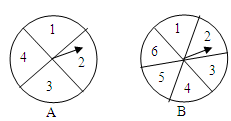
(1)同时转动转盘A与B;
(2)转盘停止后,指针各指向一个数字(如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止),用所指的两个数字作乘积,如果所得的积是偶数,那么甲胜;如果所得的积是奇数,那么乙胜.
你认为这样的规则是否公平?请你说明理由;如果不公平,请你设计一个公平的规则,并说明理由.
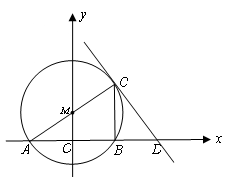
如图,在平面直角坐标系中,⊙M与x轴交于A、B两点,AC是⊙M的直径,过点C的直线交x轴于点D,连接BC,已知点M的坐标为(0, ),直线CD的函数解析式为y=-
),直线CD的函数解析式为y=- x+5
x+5 .
.
(1)点D的坐标和BC的长;
(2)求点C的坐标和⊙M的半径;
(3)求证:CD是⊙M的切线.