抛物线 交
交 轴于
轴于 两点,交
两点,交 轴于点
轴于点 ,对称轴为直线
,对称轴为直线 。且A、C两点的坐标分别为
。且A、C两点的坐标分别为 ,
,

求抛物线
 的解析式;
的解析式;在对称轴上是否存在一个点
 ,使
,使 的周长最小.若存在,请求出点
的周长最小.若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
如图,PB为⊙O的切线,B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
(1)求证:直线PA为⊙O的切线;
(2)求证:EF2=4OD•OP;
(3)若BC=6,tan∠F= ,求AC的长.
,求AC的长.
如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表: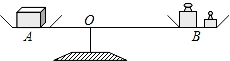
| x(cm) |
10 |
15 |
20 |
25 |
30 |
| y(g) |
30 |
20 |
15 |
12 |
10 |
(1)猜测y与x之间的函数关系,求出函数关系式并加以验证;
(2)当砝码的质量为24g时,活动托盘B与点O的距离是多少?
(3)将活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?
如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.
(1)该小组的同学在这里利用的是 投影的有关知识进行计算的;
(2)试计算出电线杆的高度,并写出计算的过程.
在阳光体育活动时间,小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.
(1)如果确定小亮打第一场,再从其余三人中随机选取一人打第一场,求恰好选中大刚的概率;
(2)如果确定小亮做裁判,用“手心、手背”的方法决定其余三人哪两人打第一场.游戏规则是:三人同时伸“手心、手背”中的一种手势,如果恰好有两人伸出的手势相同,那么这两人上场,否则重新开始,这三人伸出“手心”或“手背”都是随机的,请用画树状图的方法求小莹和小芳打第一场的概率.
已知关于x的方程x2+2(k-3)x+k2=0有两个实数根x1、x2.
(1)求k的取值范围;
(2)若|x1+x2-9|=x1x2,求k的值.