已知椭圆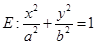 的右焦点为
的右焦点为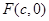 且
且 ,设短轴的一个端点为
,设短轴的一个端点为 ,原点
,原点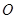 到直线
到直线 的距离为
的距离为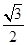 ,过原点和
,过原点和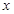 轴不重合的直线与椭圆
轴不重合的直线与椭圆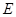 相交于
相交于 两点,且
两点,且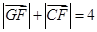 .
.
(1) 求椭圆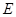 的方程;
的方程;
(2) 是否存在过点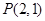 的直线
的直线 与椭圆
与椭圆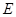 相交于不同的两点
相交于不同的两点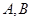 且使得
且使得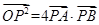 成立?若存在,试求出直线
成立?若存在,试求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分10分)选修4-5:不等式选讲
已知关于 的不等式
的不等式 。
。
(1)当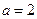 时,解上述不等式;
时,解上述不等式;
(2)如果关于 的不等式
的不等式 的解集为空
的解集为空 集,求实数
集,求实数 的取值范围。
的取值范围。
(本小题满分12分)
设函数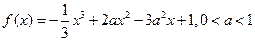 。
。
(1)求函数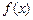 的极大值;
的极大值;
(2)若 时,恒有
时,恒有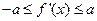 成立(其中
成立(其中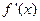 是函数
是函数 的导函数),试确定实数
的导函数),试确定实数 的取值范围。
的取值范围。
(本小题满分12分)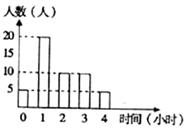
某班主任统计本班50名学生放学回家后学习时间的数据,用条形图表示(如图)。
(1)求该班学生每天在家学习时间的平均值;
(2)该班主任用公层抽样方法(按学习时间分五层)选出10个谈话,求在学习时间1个小时的学生中选出的人数;
(3)假设学生每天在家 学习时间为18时至23时,已知甲每天连续学习2小时,乙每天连续学习3小时,求22时甲、乙都在学习的概率。
学习时间为18时至23时,已知甲每天连续学习2小时,乙每天连续学习3小时,求22时甲、乙都在学习的概率。
甲方是一农场,乙方是一工厂。由于乙方生产需占用甲方的资源,因此甲方有权向乙方索赔,以弥补经济损失并获得一定净收入。在乙方不赔付甲方的情况下,乙方的年利润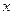 (元)与年产量
(元)与年产量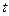 (吨)满足关系
(吨)满足关系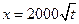 。若乙方每生产一吨产品必须赔付甲方
。若乙方每生产一吨产品必须赔付甲方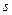 元(以下称
元(以下称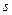 为赔付价格)
为赔付价格)
⑴将乙方的实际年利润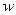 (元)表示为年产量
(元)表示为年产量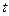 (吨)的函数,并求乙方获得最大年利润时的年产量;
(吨)的函数,并求乙方获得最大年利润时的年产量;
⑵甲方每年受乙方生产影响的经济损失金额为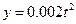 (元),在乙方按照获得最大年利润时的年产量的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格
(元),在乙方按照获得最大年利润时的年产量的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格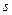 是多少?
是多少?
设函数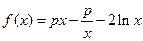 。
。
⑴若函数 在其定义域内为单调递增函数,求
在其定义域内为单调递增函数,求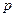 的取值范围;
的取值范围;
⑵设 且
且 ,若在
,若在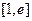 上至少存在一点
上至少存在一点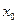 ,使得
,使得 成立,求实数
成立,求实数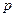 的取值范围。
的取值范围。