如图,三棱锥P—ABC中, 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD 平面PAB。
平面PAB。
(1)求证: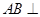 平面PCB;
平面PCB;
(2)求二面角C—PA—B的余弦值。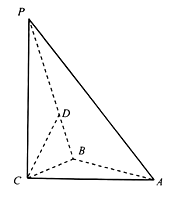
(本小题满分16分)设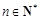 ,函数
,函数
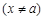 ,其中常数a
,其中常数a .
.
(1)求函数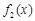 的极值;
的极值;
(2)设一直线与函数 的图象切于两点A(x1,y1),B(x2,y2),且
的图象切于两点A(x1,y1),B(x2,y2),且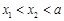 .
.
①求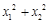 的值;
的值;
②求证: .
.
(本小题满分16分) 如图,过椭圆 的左顶点
的左顶点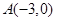 和下顶点
和下顶点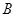 且斜率均为
且斜率均为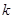 的两直线
的两直线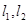 分别交椭圆于
分别交椭圆于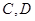 ,又
,又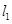 交
交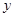 轴于
轴于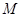 ,
,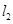 交
交 轴于
轴于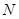 ,且
,且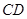 与
与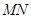 相交于点
相交于点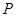 .当
.当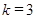 时,
时,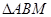 是直角三角形.
是直角三角形.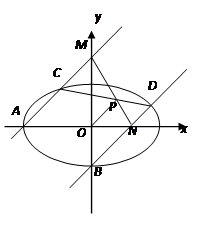
(1)求椭圆L的标准方程;
(2)①证明:存在实数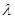 ,使得
,使得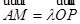 ;
;
②求|OP|的最小值.
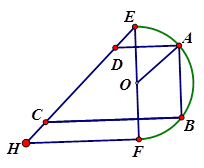
(本小题满分14分)为了制作广告牌,需在如图所示的铁片上切割出一个直角梯形,已知铁片由两部分组成,半径为1的半圆O及等腰直角三角形EFH,其中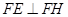 。为裁剪出面积尽可能大的梯形铁片ABCD(不计损耗),将点A,B放在弧EF上,点C、D放在斜边
。为裁剪出面积尽可能大的梯形铁片ABCD(不计损耗),将点A,B放在弧EF上,点C、D放在斜边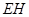 上,且
上,且 ,设
,设 .
.
(1)求梯形铁片ABCD的面积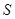 关于
关于 的函数关系式;
的函数关系式;
(2)试确定 的值,使得梯形铁片ABCD的面积
的值,使得梯形铁片ABCD的面积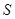 最大,并求出最大值.
最大,并求出最大值.
(本小题满分14分)在三棱锥P-SBC中,A,D分别为边SB,SC的中点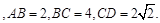 平面PSB
平面PSB 平面ABCD,平面PAD
平面ABCD,平面PAD 平面ABCD
平面ABCD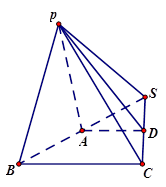
(1)求证:PA⊥BC;
(2)若平面PAD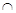 平面PBC=
平面PBC=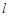 ,求证:
,求证: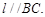
已知向量 ,
,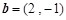 .
.
(1)若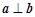 ,求
,求 的值;
的值;
(2)若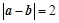 ,
,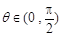 ,求
,求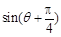 的值
的值