(本小题满分12分)
已知函数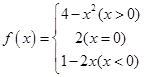 ,
,
(Ⅰ)画出函数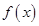 图像;
图像;
(Ⅱ)求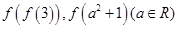 的值;
的值;
(Ⅲ)当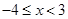 时,求
时,求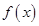 取值的集合.
取值的集合.
某校高三某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下图,据此解答如下问题: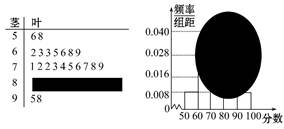
(1)求分数在[50,60)的频率及全班的人数.
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高.
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份在[90,100]之间的概率.
已知(1+x+mx2)10的展开式中x4的系数大于-330,求m的取值范围.
20个相同的小球,全部装入编号为1,2,3的三个盒子里,每个盒子内所放的球数不小于盒子的编号数,求共有多少种不同的放法?
已知10件不同产品中共有4件次品,现对它们进行一一测试,直至找到所有次品为止.
(1)若恰在第5次测试,才测试到第一件次品,第10次才找到最后一件次品的不同测试方法数有多少种?
(2)若恰在第5次测试后,就找出了所有次品,则这样的不同测试方法数有多少种?
某城市在中心广场建造一个花圃,花圃分为6个部分(如图).现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有多少种(用数字作答).