观察下面三行数
1，－2，4，－8，16，－32 …… ①
0，－6，6，－18，30，－66 …… ②
2，－4，8，－16，32，－64 …… ③第③行的数按什么规律排列？
第①、②行的数与第③行的数分别有什么关系？
取每行数的第8个数，计算它们的和。
如图①所示是一个长为2m，宽为2n的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的方式拼成一个正方形.
图②中的阴影部分的正方形的边长等于_________________．
请用两种不同的方法列代数式表示图②中阴影部分的面积：
方法①_________________________________________________________．
方法②_________________________________________________________．观察图②，写出(m＋n)2、(m－n)2、mn这三个代数式之间的等量关系．
根据(3)题中的等量关系，解决问题：已知a＋b＝6，ab＝4，求(a－b)2的值
某城市按以下规定收取每月煤气费：用煤气不超过60立方米，按每立方米0.8元收费；如果超过60立方米，超过部分按每立方米1.2元收费. 如甲用户某月份用煤气80每立方米，那么这个月甲用户应交煤气费用为60×0.8＋（80－60）×1.2＝72元.设甲用户某月用煤气x立方米，用含x的代数式表示甲用户该月的煤气费.
若x≤60,则费用表示为;
若x＞60,则费用表示为.若甲用户10月份的煤气费是84元，求甲用户10月份用去煤气多少立方米?
某自行车厂计划一周生产自行车1400辆，平均每天生产200辆，但由于种种原因，实际每天生产量与计划量相比有出入. 下表是某周的生产情况（超产记为正、减产记为负）：
根据记录的数据可知该厂星期四生产自行车辆；
根据记录的数据可知该厂本周实际生产自行车辆；
产量最多的一天比产量最少的一天多生产自行车辆
该厂实行每周计件工资制，每生产一辆车可得30元，若超额完成任务，则超过部分每辆另奖20元；少生产一辆扣15元，那么该厂工人这一周的工资总额是多少元？
化简3x2＋2x－5x2＋3x
4(m2＋n)＋2(n－2m2)
－3(2x2－xy)－(x2＋xy－6)
－(6a3b＋2b2)＋(4a3b－8b2)
先化简，再求值：3x2y－[2x2y－(2xy－3x2y)]＋3xy2，其中x＝3，y＝－
阅读下面的文字，解答问题：
大家都知道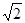
是无理数，而且
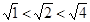，即
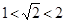，无理数是无限不循环小数，因此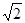的小数部分我们不可能全部地写出来，于是小明用
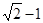来表示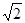的小数部分，你同意小明的表示方法吗？事实上，小明的表示方法是有道理，因为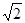的整数部分是1，将这个数减去其整数部分，差就是小数部分.
又例如：①∵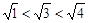
，即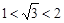
，
∴
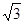的整数部分为1，小数部分为
.
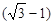②∵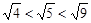
，即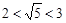
，
∴
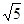的整数部分为2，小数部分为
.
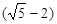请解答：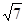
的整数部分为，小数部分为。如果
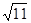的小数部分为a，
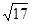的整数部分为b，求
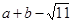的值；（要求写出解题过程）