已知椭圆C: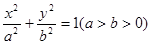 的两个焦点为
的两个焦点为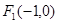 、
、
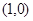 ,且经过点
,且经过点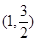 ,一组斜率为
,一组斜率为 的直线与椭圆C都相交于不同两点
的直线与椭圆C都相交于不同两点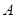 、
、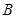 。
。
(1)求椭圆C的方程;
(2)证明:线段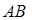 的中点都有在同一直线
的中点都有在同一直线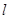 上;
上;
(3)对于(2)中的直线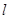 ,设
,设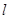 与椭圆C交于两点M、N,试探究椭圆上使
与椭圆C交于两点M、N,试探究椭圆上使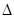 MNQ面积为
MNQ面积为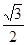 的点Q有几个?证明你的结论。(不必具体求出Q点的坐标)
的点Q有几个?证明你的结论。(不必具体求出Q点的坐标)
平面直角坐标系中,O为坐标原点,给定两点A(1,0)、B(0,-2),点C满足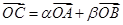 ,其中
,其中 ,且
,且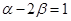
(1)求点C的轨迹方程;(2)设点C的轨迹与双曲线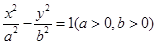 交于两点M、N,且以MN为直径的圆过原点,若双曲线的离心率不大于
交于两点M、N,且以MN为直径的圆过原点,若双曲线的离心率不大于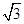 ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围.
设正数数列 的前n次之和为
的前n次之和为 满足
满足 =
=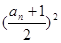
①求 ,
,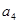 ②猜测数列
②猜测数列 的通项公式,并用数学归纳法加以证明
的通项公式,并用数学归纳法加以证明
③设 ,数列
,数列 的前n项和为
的前n项和为 ,求
,求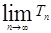 的值.
的值.
已知函数 .
.
(1) 当m=0时,求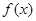 在区间
在区间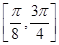 上的取值范围;
上的取值范围;
(2) 当 时,
时, ,求m的值.
,求m的值.
如图,在以点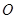 为圆心,
为圆心,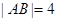 为直径的半圆
为直径的半圆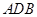 中,
中,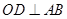 ,
,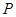 是半圆弧上一点,
是半圆弧上一点,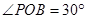 ,曲线
,曲线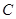 是满足
是满足 为定值的动点
为定值的动点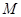 的轨迹,且曲线
的轨迹,且曲线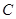 过点
过点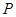 .
.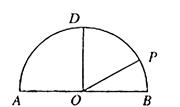
(Ⅰ)建立适当的平面直角坐标系,求曲线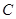 的方程;
的方程;
(Ⅱ)设过点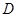 的直线l与曲线
的直线l与曲线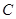 相交于不同的两点
相交于不同的两点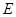 、
、
若△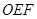 的面积不小于
的面积不小于 ,求直线
,求直线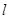 斜率的取值范围.
斜率的取值范围.
已知数列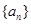 和
和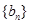 满足:
满足: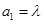 ,
,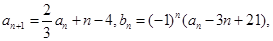 其中
其中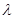 为实数,
为实数,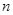 为正整数.
为正整数.
(Ⅰ)对任意实数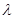 ,证明数列
,证明数列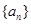 不是等比数列;
不是等比数列;
(Ⅱ)试判断数列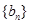 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
(Ⅲ)设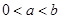 ,
, 为数列
为数列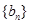 的前
的前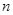 项和.是否存在实数
项和.是否存在实数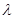 ,使得对任意正整数
,使得对任意正整数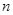 ,都有
,都有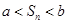 ?若存在,求
?若存在,求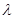 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.