已知向量p＝(－cos2x，a)，q＝(a,2

题文

已知向量p＝(－cos 2x，a)，q＝(a,2－sin 2x)，函数f(x)＝p·q－5(a∈R，a≠0)
(1)求函数f(x)(x∈R)的值域；
(2)当a＝2时，若对任意的t∈R，函数y＝f(x)，x∈(t，t＋b]的图像与直线y＝－1有且仅有两个不同的交点，试确定b的值(不必证明)，并求函数y＝f(x)的在[0，b]上单调递增区间．

科目数学题型解答题难度容易

登录免费查看答案和解析

相关试题

设常数 $a \geq 0$ ，函数 $f (x) = \frac{2^{x} + a}{2^{x} - a}$ 若 $a$ =4，求函数 $y = f (x)$ 的反函数 $y = f^{- 1} (x)$ ；
根据 $a$ 的不同取值，讨论函数 $y = f (x)$ 的奇偶性，并说明理由.

底面边长为2的正三棱锥 $P - A B C$ ,其表面展开图是三角形 $P_{1} P_{2} P_{3}$ ，如图，求△ $P_{1} P_{2} P_{3}$ 的各边长及此三棱锥的体积 $V$ .

设函数 $f (x) = \ln x + \frac{m}{x}, m \in R$ .
（1）当 $m = e$ （ $e$ 为自然对数的底数）时，求 $f (x)$ 的最小值；
（2）讨论函数 $g (x) = f ` (x) - \frac{x}{3}$ 零点的个数；
（3）若对任意 $b > a > 0, \frac{f (b) - f (a)}{b - a} < 1$ 恒成立，求 $m$ 的取值范围.

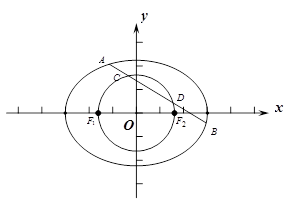
已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 经过点 $(0, \sqrt{3})$ ，离心率为 $\frac{1}{2}$ ，左右焦点分别为 $F_{1} (- c, 0), F_{2} (c, 0)$ .

（1）求椭圆的方程；
（2）若直线 $l : y = - \frac{1}{2} x + m$ 与椭圆交于 $A, B$ 两点，与以 $F_{1} F_{2}$ 为直径的圆交于 $C, D$ 两点，且满足 $\frac{|A B|}{|C D|} = \frac{5 \sqrt{3}}{4}$ ，求直线 $l$ 的方程.

某保险公司利用简单随机抽样方法，对投保车辆进行抽样，样本车辆中每辆车的赔付结果统计如下：

赔付金额（元）	0	1000	2000	3000	4000
车辆数（辆）	500	130	100	150	120

（1）若每辆车的投保金额均为2800元，估计赔付金额大于投保金额的概率；
（2）在样本车辆中，车主是新司机的占10℅，在赔付金额为4000元的样本车辆中，车主是新司机的占20℅，估计在已投保车辆中，新司机获赔金额为4000元的概率.

试卷网试题网古诗词网作文网范文网