南昌市教育局组织中学生足球比赛,共有实力相当的8支代表队(含有一中代表队,二中代表队)参加比赛,比赛规则如下:
第一轮:抽签分成四组,每组两队进行比赛,胜队进入第二轮,第二轮:将四队分成两组,每组两队进行比赛,胜队进入第三轮,第三轮:两队进行决赛,胜队获得冠军。
现记ξ=0表示整个比赛中一中代表队与二中代表队没有相遇,ξ=i表示恰好在第i轮比赛时一中代表队,二中代表队相遇(i=1,2,3).
(1)求ξ的分布列;
(2)求Eξ.
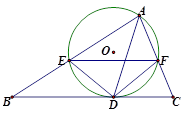
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,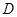 是AC的中点,已知
是AC的中点,已知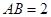 ,
,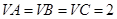 .
.
(1)求证:AC⊥平面VOD;
(2)求三棱锥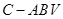 的体积.
的体积.
数列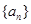 的前
的前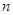 项和为
项和为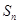 ,且
,且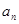 是
是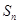 和
和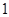 的等差中项,等差数列
的等差中项,等差数列 满足
满足 ,
, .
.
(1)求数列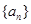 、
、 的通项公式;
的通项公式;
(2)设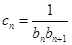 ,数列
,数列 的前
的前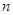 项和为
项和为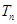 ,证明:
,证明: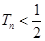 .
.
已知函数 (a是常数,a∈R)
(a是常数,a∈R)
(1)当a=1时求不等式 的解集.
的解集.
(2)如果函数 恰有两个不同的零点,求a的取值范围.
恰有两个不同的零点,求a的取值范围.
已知曲线 (
( 为参数),曲线
为参数),曲线 ,将
,将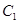 的横坐标伸长为原来的2倍,纵坐标缩短为原来的
的横坐标伸长为原来的2倍,纵坐标缩短为原来的 得到曲线
得到曲线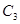 .
.
(1)求曲线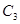 的普通方程,曲线
的普通方程,曲线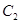 的直角坐标方程;
的直角坐标方程;
(2)若点P为曲线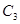 上的任意一点,Q为曲线
上的任意一点,Q为曲线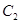 上的任意一点,求线段
上的任意一点,求线段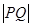 的最小值,并求此时的P的坐标.
的最小值,并求此时的P的坐标.
如图,在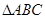 中,
中,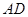 是的∠A的平分线,圆
是的∠A的平分线,圆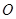 经过点
经过点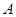 与
与 切于点
切于点 ,与
,与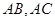 相交于
相交于 ,连结
,连结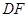 ,
, .
.
(1)求证: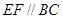 ;(2)求证:
;(2)求证: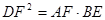 .
.