已知函数f(x)=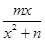 (m,n∈R)在x=1处取到极值2.
(m,n∈R)在x=1处取到极值2.
(1)求f(x)的解析式;
(2)设函数g(x)=ax-lnx.若对任意的x1∈[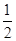 ,2],总存在唯一的x2∈[
,2],总存在唯一的x2∈[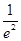 ,e](e为自然对数的底),使得g(x2)=f(x1),求实数a的取值范围.
,e](e为自然对数的底),使得g(x2)=f(x1),求实数a的取值范围.
已知函数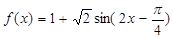 。
。
(1)求函数的最小正周期和最大值;
(2)求函数的增区间;
(3)函数的图象可以由函数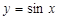 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
已知向量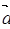 =(
=(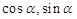 ),
),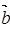 =(
=(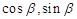 ).
).
(1)当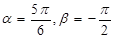 时,求
时,求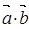 的值。
的值。
(2)已知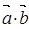 =
=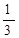 ,
,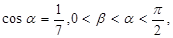 求
求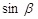 的值。
的值。
已知函数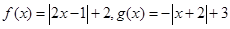
(1)解不等式: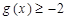 ;
;
(2)若关于x的不等式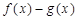 ≥m+2的解集为R,求实数m的取值范围.
≥m+2的解集为R,求实数m的取值范围.
已知函数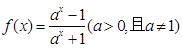 ,设函数
,设函数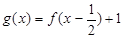
(1)求证: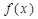 是奇函数;
是奇函数;
(2)①求证: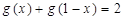 ;
;
②结合①的结论求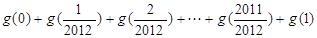 的值;
的值;
(3)仿上,设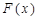 是
是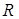 上的奇函数,请你写出一个函数
上的奇函数,请你写出一个函数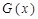 的解析式,并根据第(Ⅱ)问的结论,猜想函数
的解析式,并根据第(Ⅱ)问的结论,猜想函数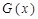 满足的一般性结论.
满足的一般性结论.
抛物线 的焦点为
的焦点为 ,
,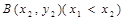 在抛物线上,
在抛物线上,
(1)存在实数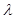 ,使
,使 ,求直线
,求直线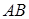 的方程;
的方程;
( 2 )以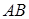 为直径的圆过
为直径的圆过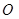 点,证
点,证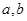 明直线
明直线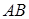 过定点,并求出定点坐标.
过定点,并求出定点坐标.