设函数 ,
,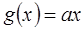 ,
,
(1)若 是
是 的极值点,求
的极值点,求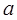 的值;
的值;
(2)在(1)的条件下,若存在 ,使得
,使得 ,求
,求 的最小值;
的最小值;
(3)若对任意的 ,
,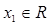 ,都有
,都有 恒成立,求
恒成立,求 的取值范围。
的取值范围。
某城市2001年底人口为500万,人均住房面积为6 m2,如果该城市每年人口平均增长率为1%,则从2002年起,每年平均需新增住房面积为多少万m2,才能使2020年底该城市人均住房面积至少为24m2?(可参考的数据1.0118=1.20,1.0119=1.21,1.0120=1.22).
已知:等差数列{ }中,
}中,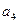 =14,前10项和
=14,前10项和 .
.
(1)求 ;
;
(2)将{ }中的第2项,第4项,…,第
}中的第2项,第4项,…,第 项按原来的顺序排成一个新数列,求此数列的前
项按原来的顺序排成一个新数列,求此数列的前 项和
项和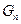 .
.
在等比数列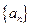 中,
中,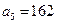 ,公比
,公比 ,前
,前 项和
项和 ,求首项
,求首项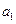 和项数
和项数
)已知x、y满足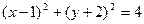 ,求
,求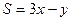 的最值
的最值
已知直线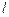 经过点P(1,1),
经过点P(1,1),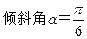 。
。
(1)写出直线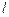 的参数方程;
的参数方程;
(2)设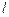 与圆
与圆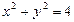 相交于两点A、B,求点P到A,B两点的距离之积
相交于两点A、B,求点P到A,B两点的距离之积