在
中，
、
、
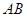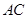三边的长分别为
、
、
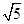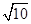，求这个三角形的面积．
小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点（即三个顶点都在小正方形的顶点处），如图
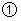所示．这样不需求的高，而借用网格就能计算出它的面积．
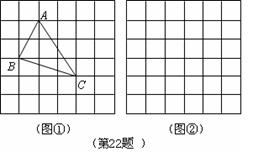
请你将
的面积直接填写在横线上．__________________
思维拓展我们把上述求
面积的方法叫做构图法．若三边的长分别为
、
、
（
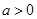），请利用图
的正方形网格（每个小正方形的边长为
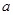）画出相应的，并求出它的面积．
探索创新：若
三边的长分别为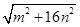
、
、
（
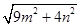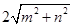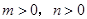，且
），试运用构图法求出这三角形的面积．
解下列方程
（1）
；
（2）
（本题14分）如图①，直线
：
分别与
轴、
轴交于A、B两点，与直线
：
交于点
．
（1）求A、B两点坐标及
、
的值；
（2）如图②，在线段BC上有一点E，过点E作轴的平行线交直线于点F，过E、F分别作EH⊥轴，FG⊥轴，垂足分别为H、G，设点E的横坐标为
，当为何值时，矩形EFGH的面积为
；
（3）若点P为轴上一点，则在平面直角坐标系中是否存在一点Q，使得P、Q、A、B四个点能构成一个菱形．若存在，求出所有符合条件的Q点坐标；若不存在，请说明理由．
（本题10分）已知如图：点（1，3）在函数
（x＞0）的图象上，矩形ABCD的边BC在x轴上，E是对角线BD的中点，函数（x＞0）的图象又经过A、E两点，点E的横坐标为m．
（1）求k的值；
（2）求点A的坐标；（用含m代数式表示）
（3）当∠ABD=45°时，求m的值．
（本题10分）某超市如果将进货价为40元的商品按50元销售，就能卖出500个，但如果这种商品每个涨价1元，其销售量就减少10个，如果你是超市的经理，为了赚得8 000元的利润，你认为售价（售价不能超过进价的160%）应定为多少？这时应进货多少个？
（本题10分）阅读材料：分解因式：
解：
=
=
=
=
=
，
此种方法抓住了二次项和一次项的特点，然后加一项，使三项成为完全平方式，我们把这种分解因式的方法叫配方法．
（1）用上述方法分解因式：
；
（2）无论
取何值，代数式
总有一个最小值，请尝试用配方法求出当取何值时代数式的值最小，并求出这个最小值．