某电子商投产一种新型电子产品，每件制造成本为18元，试销过程发现，每月销量
y（万件）与销售单价x（元）之间的关系可以近似地看作一次函数y=-2x+100．
（1）写出每月的利润z（万元）与销售单价x（元）之间函数解析式；
（2）当销售单价为 多少元时，厂商每月能够获得350万元的利润？当销售单价为多少元时，厂商每月能够获得最大利润？最大利润是多少？
（3）根据相关部门规定，这种电子产品的销售单价不得高于32元．如果厂商要获得每月不低于350万元的利润，那么制造这种产品每月的最低制造成本需要多少万元？
(本题满分12分)已知AB是⊙O的一条弦，CD是⊙O的直径，CD⊥AB，垂足为K．现取一块三角板，把它的一个锐角顶点固定在点C处，该锐角的两边(从左到右)与直线AB和圆分别相交于E、F和G、H．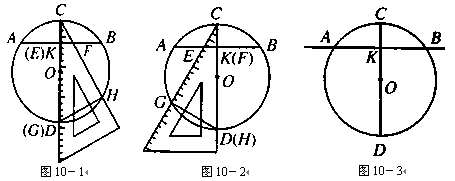
(1) 若∠C的一边过圆心，请选择图10-1或图10-2所示，求证： △CEF∽△CHG；
(2) 若∠C的边不过圆心，在图10-3中补全一种示意图，请你观察所画的图形，并判断(1)中的结论是否仍然成立？若成立，给予证明；若不成立，请说明理由．
(本题满分12分)
节假日，小明和哥哥在水族馆看完海洋动物后，参加了出口处的抽奖活动．游戏的规则如下：每张门票只可摸球一次，每次从装有大小形状相同的2个白球和1个红球的盒子中，随机摸出一个球，若摸出的是红球，则获得一份奖品．(1) 求每次摸球中奖的概率？
(2) 小明想：我有二张票，中奖的概率就翻一倍．你认为小明的思考正确吗？请用列表法或画树形图分析说明．
(本题满分12分)已知关于x的一元二次方程x2－3x＋m＝0．(1) 当m为何值时，方程有两个相等的实数根；
(2) 当
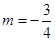时，求方程的正根．
(本题满分12分)
如图，在4×4的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上．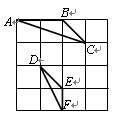
(1) 填空：∠ABC＝___________°，BC＝_________；
(2) 判断△ABC与△DEF是否相似，并证明你的结论．
(本题满分10分)
已知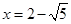
，
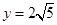，求
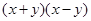的值．