(本小题满分12分)
一个多面体的直观图和三视图如图所示:
(I)求证:PA⊥BD;
(II)连接AC、BD交于点O,在线段PD上是否存在一点Q,使直线OQ与平面ABCD所成的角为30o?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知函数 .

(1)画出 和
和
 图像;
图像;
(2)若 ,求a的取值范围.
在直角坐标系 中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为 .
(1)将C的极坐标方程化为直角坐标方程;
(2)设点A的直角坐标为 ,M为C上的动点,点P满足 ,写出Р的轨迹 的参数方程,并判断C与 是否有公共点.
抛物线C的顶点为坐标原点O.焦点在x轴上,直线l: 交C于P,Q两点,且 .已知点 ,且 与l相切.
(1)求C, 的方程;
(2)设 是C上的三个点,直线 , 均与 相切.判断直线 与 的位置关系,并说明理由.
设函数 ,其中 .
(1)讨论 的单调性;
(2)若 的图像与
轴没有公共点,求a的取值范围.
的图像与
轴没有公共点,求a的取值范围.
已知直三棱柱
中,侧面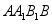 为正方形,
,E,F分别为
和
的中点,
.
为正方形,
,E,F分别为
和
的中点,
.

(1)求三棱锥 的体积;
(2)已知D为棱 上的点,证明: .