（本小题满分14分）
设椭圆C：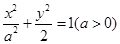
的左、右焦点分别为F1、F2，A是椭圆C上的一点，
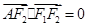,坐标原点O到直线AF1的距离为
.
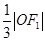(Ⅰ)求椭圆C的方程；
(Ⅱ)设Q是椭圆C上的一点，过点Q的直线l 交 x轴于点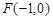
，交 y轴于点M，若
,求直线l 的斜率.
（本小题满分12分）
已知p：方程x2＋mx＋1＝0有两个不相等的负实根；q：不等式4x2＋4(m－2)x＋1＞0的解集为R，若p或q为真命题，p且q为假命题，求m的取值范围．
（本小题满分12分）已知9x－10·3x+9≤0，求函数y=（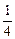
）x－1－4（
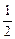）x+2的最大值和最小值，并指出取得最值时x的
值
（本小题满分14分）已知函数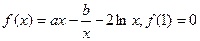
．
（Ⅰ）若函数f(x)在其定义域内为单调函数，求a的取值范围；
（Ⅱ）若函数f(x)的图象在x = 1处的切线的斜率为0，且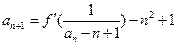
，已
知a1 = 4，求证：an³ 2n + 2；
（Ⅲ）在（Ⅱ）的条件下，试比较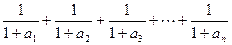
与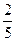
的大小，并说明你的理由．
（本小题满分13分）
定长为3的线段AB两端点A、B分别在
轴，
轴上滑动，M在线段AB上，且
（1）求点M的轨迹C的方程；
（2）设过
且不垂直于坐标轴的动直线
交轨迹C于A、B两点，问：线段
上
是否存在一点D，使得以DA，DB为邻边的平行四边形为菱形？作出判断并证明。
（本小题满分12分）已知函数
（1）求函数
的最大值；
（2）当
时，求证
；