设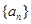 是等差数列,
是等差数列,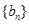 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且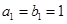 ,
,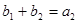 ,
, 。
。
(1)求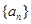 ,
,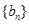 的通项公式;
的通项公式;
(2)求数列 的前n项和
的前n项和 .
.
有一块直角三角形木板,如图所示,∠C=90°,AB=5 cm,BC=3 cm,AC=4 cm,根据需要,要把它加工成一个面积最大的正方形木板,设计一个方案,应怎样裁才能使正方形木板面积最大,并求出这个正方形木板的边长.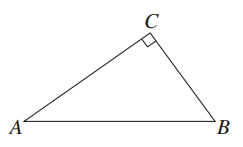
如图所示,已知,在边长为1的正方形ABCD的一边上取一点E,使AE=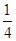 AD,从AB的中点F作HF⊥EC于H.
AD,从AB的中点F作HF⊥EC于H.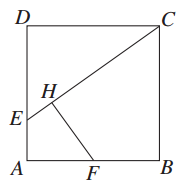
(1)求证:FH=FA;
(2)求EH∶HC的值.
如图,△ABC中,AB=AC,∠BAC=90°,AE=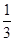 AC,BD=
AC,BD=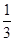 AB,点F在BC上,且CF=
AB,点F在BC上,且CF=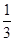 BC.求证:
BC.求证: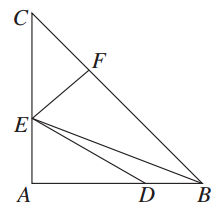
(1)EF⊥BC;
(2)∠ADE=∠EBC.
如图,△ABC中,AB=AC,AD是中线,P为AD上一点,CF∥AB,BP延长线交AC、CF于E、F,求证:PB2=PE·PF.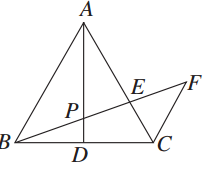
某企业为加大对新产品的推销力度,决定从今年起每年投入100万元进行广告宣传,以增加新产品的销售收入.已知今年的销售收入为250万元,经市场调查,预测第n年与第n-1年销售收入an与an-1(单位:万元)满足关系式:an=an-1+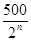 -100.
-100.
(1)设今年为第1年,求第n年的销售收入an;
(2)依上述预测,该企业前几年的销售收入总和Sn最大.