如图所示,在平面直角坐标系中,矩形ABOC的边OB在x轴的负半轴上,边OC在y轴的正半轴上,且AB=1,OB=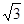 ,矩形ABOC绕点O按顺时针方向旋转60°后得矩形EFOD. 点A的对应点为点E,点B的对应点为F,点C的对应点为点D. 抛物线
,矩形ABOC绕点O按顺时针方向旋转60°后得矩形EFOD. 点A的对应点为点E,点B的对应点为F,点C的对应点为点D. 抛物线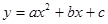 过点A、E、D.
过点A、E、D.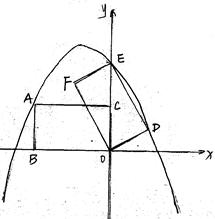
(1) 判断点E是否在y轴上,并说明理由;
(2)求抛物线的解析式;
(3)在x 轴的上方是否存在点P、Q,使以点O、B、P、Q为顶点的平行四边形的面积是矩形ABOC的面积的2倍,且点P在抛物线上,若存在,求P、Q两点的坐标,若不存在,请说明理由。
设等式 在实数范围内成立,其中 是两两不同的实数,求 的值.
如图,在 中, 于 于 是 的角平分线,求证: .
一只青蛙在平面直角坐标系上从点 开始,可以按照如下两种方式跳跃:①能从任意一点 ,跳到点 或 ;②对于点 ,如果 ,则能从 跳到 ,如果 ,则能从 跳到 ,例如,按照上述跳跃方式,这只青蛙能够到达点 ,跳跃的一种路径为: ,请你思考:这只青蛙按照规定的两种方式跳跃,能达到下列各点吗?如果能,请分别给出从点 出发到指定点的路径;如果不能,请说明理由.
(1) ;(2) ;(3) ;(4) .
如果将点 绕定点 旋转 后与点 重合,那么称点 与点 关于点 对称,定点 叫对称中心,此时,点 是线段 的中点,如图,在直角坐标系中, 的顶点 的坐标分别为 ,点列 中的相邻两点都关于 的一个顶点对称,点 与点 关于点 对称,点 与点 关于点 对称,点 与点 关于点 对称,点 与点 关于点 对称,点 与点 关于点 对称,点 与点 关于点 对称,…,对称中心分别是 ,且这些对称中心依次循环,已知 的坐标为 ,试写出 的坐标.
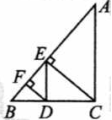
如图,已知:在平面直角坐标系中,四边形 是长方形, 点与原点重合,坐标为 .
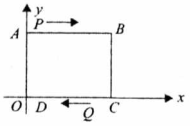
(1)写出点 的坐标;
(2)动点 从点 出发以每秒 个单位长度的速度向终点 运动,动点 从点 出发以每秒 个单位长度的速度沿射线 方向匀速运动,若 两点同时出发,设运动时间为 秒,当 为何值时, ?
(3)在点 的运动过程中,当点 运动到什么位置时,使 ?求出此时 点的坐标.