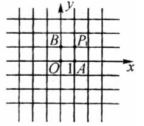
如果将点 绕定点 旋转 后与点 重合,那么称点 与点 关于点 对称,定点 叫对称中心,此时,点 是线段 的中点,如图,在直角坐标系中, 的顶点 的坐标分别为 ,点列 中的相邻两点都关于 的一个顶点对称,点 与点 关于点 对称,点 与点 关于点 对称,点 与点 关于点 对称,点 与点 关于点 对称,点 与点 关于点 对称,点 与点 关于点 对称,…,对称中心分别是 ,且这些对称中心依次循环,已知 的坐标为 ,试写出 的坐标.
为了经济发展的需要,某市2014年投入科研经费500万元,2016年投入科研经费720万元.
(1)求2014至2016年该市投入科研经费的年平均增长率;
(2)根据目前经济发展的实际情况,该市计划2017年投入的科研经费比2016年有所增加,但年增长率不超过15%,假定该市计划2017年投入的科研经费为a万元,请求出a的取值范围.
在国务院办公厅发布《中国足球发展改革总体方案》之后,某校为了调查本校学生对足球知识的了解程度,随机抽取了部分学生进行一次问卷调查,并根据调查结果绘制了如图的统计图,请根据图中所给的信息,解答下列问题:
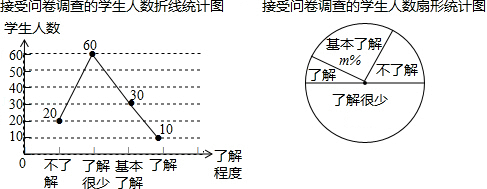
(1)本次接受问卷调查的学生总人数是 ;
(2)扇形统计图中,“了解”所对应扇形的圆心角的度数为 ,m的值为 ;
(3)若该校共有学生1500名,请根据上述调查结果估算该校学生对足球的了解程度为“基本了解”的人数.
如图,已知一次函数 的图象与反比例函数 的图象交于点A(﹣1,2)和点B,点C在y轴上.
(1)当△ABC的周长最小时,求点C的坐标;
(2)当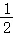 x+b<
x+b<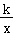 时,请直接写出x的取值范围.
时,请直接写出x的取值范围.
如图,在▱ABCD中,AC为对角线,AC=BC=5,AB=6,AE是△ABC的中线.
(1)用无刻度的直尺画出△ABC的高CH(保留画图痕迹);
(2)求△ACE的面积.

(1)计算: ;
(2)解分式方程: .