(本小题满分10分)选修4-5:不等式选讲
设函数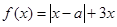 ,其中
,其中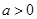 .
.
(Ⅰ)当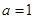 时,求不等式
时,求不等式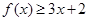 的解集;
的解集;
(Ⅱ)若不等式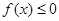 的解集为
的解集为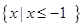 ,求a的值.
,求a的值.
(本题满分为12分)
已知函数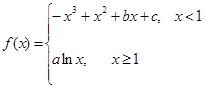 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点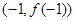 处的切线
处的切线
的斜率是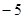 .
.
(1)求实数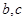 的值;(2)求
的值;(2)求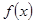 在区间
在区间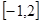 上的最大值;
上的最大值;
(本题满分为12分)已知椭圆中心在原点,焦点在y轴上,焦距为4,离心率为 .
.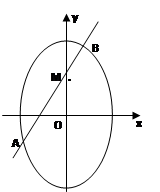
(I)求椭圆方程;
(II)设椭圆在y轴的正半轴上的焦点为M,又点A和点B在椭圆上,且M分有向线段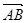 所成的比为2,求线段AB所在直线的方程.
所成的比为2,求线段AB所在直线的方程.
(本小题满分12分)某饮料公司招聘了一名员工,现对其进行一项测试,以使确定工资级别,公司准备了两种不同的饮料共8杯,其颜色完全相同,并且其中4杯为A饮料,另外4杯为B饮料,公司要求此员工一一品尝后,从8杯饮料中选出4杯A饮料,若4杯都选对,则月工资定为3500元,若4杯选对3杯,则月工资定为2800元,否则月工资定为2100元,令X表示此人选对A饮料的杯数,假设此人对A和B两种饮料没有鉴别能力.
(1)求X的分布列;
(2)求此员工月工资的期望.
(本小题满分12分)如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(Ⅰ)证明:PA⊥BD;
(Ⅱ)若PD=AD,求二面角A-PB-C的余弦值.