“低碳经济”是促进社会可持续发展的推进器.某企业现有100万元资金可用于投资，如果投资“传统型”经济项目，一年后可能获利20%，可能损失10%,也可能不赔不赚，这三种情况发生的概率分别为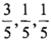
；如果投资“低碳型”经济项目，一年后可能获利30%,也
可能损失20%，这两种情况发生的概率分别为a和n (其中a + b =1 )如果把100万元投资“传统型”经济项目，用
表示投资收益（投资收益=回收资金一投资资金)，求
的概率分布及均值（数学期望）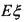
；(II)如果把100万元投资“低碳型”经济项目，预测其投资收益均值会不低于投资“传统型”经济项目的投资收益均值，求a的取值范围
已知
为椭圆
的左右焦点，
是坐标原点，过
作垂直于
轴的直线
交椭圆于
，设
.
（1）证明：
成等比数列；
(2)若的坐标为
，求椭圆
的方程；
（3）在(2)的椭圆中，过
的直线
与椭圆交于
、
两点，若
，求直线的方程．
如图，在四棱锥
中，
底面
，底面是平行四边形，
，
是
的中点。
（1）求证：
；
（2）求证：
；
（3）若
，求二面角
的余弦值．
已知以角
为钝角的
的内角
的对边分别为
、
、
，
，且
与
垂直。
（1）求角的大小；
（2）求
的取值范围．
在某次测验中，有6位同学的平均成绩为75分．用
表示编号为
（
）的同学所得成绩，且前5位同学的成绩如下：70,76,72,70,72.
(1)求第6位同学的成绩
，及这6位同学成绩的标准差
；
(2)从前5位同学中，随机地选2位同学，求恰有1位同学成绩在区间(68,75)中的概率．
已知数列
是等差数列，且
.
（1）求数列的通项公式;（2）令
，求数列
前n项和
.