己知函数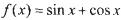 .
.
(I )若,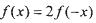 ,求
,求 的值;
的值;
(II)求函数 的最大值和单调递增区间.
的最大值和单调递增区间.
(本小题满分12分)
已知函数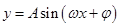 ,
, (其中A>0,
(其中A>0, >0,
>0, <
<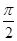
 的部分图象如图所示,求这个函数的解析式.
的部分图象如图所示,求这个函数的解析式.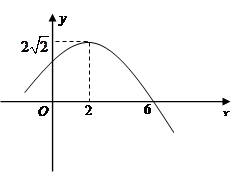
(本小题满分12分)
已知 ,
, ,求
,求 的值.
的值.
(满分13分)已知各项均为正数的数列 是数列
是数列 的前n项和,对任意
的前n项和,对任意 ,有2Sn=2
,有2Sn=2 .
.
(Ⅰ)求常数p的值;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)记 ,(
,( )若数列
)若数列 从第二项起每一项都比它的前一项大,求
从第二项起每一项都比它的前一项大,求 的取值范围.
的取值范围.
(满分13分)某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成。已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米。
(1)若设休闲区的长 米,求公园ABCD所占面积S关于
米,求公园ABCD所占面积S关于 的函数
的函数 的解析式;
的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
(满分13分)设正项等比数列 的前
的前 项和为
项和为 , 已知
, 已知 ,
, .
.
(1)求首项 和公比
和公比 的值;(2)试证明数列
的值;(2)试证明数列 为等差数列.
为等差数列.